Воздействие - скачок
Cтраница 2
Напомним, что при околозвуковых режимах резко возрастают продольные градиенты давления. Повторный отрыв слоя происходит под воздействием скачка IV у выходной кромки. [16]
Кроме того, иногда используются параметры, представляющие собой скорость нарастания и время установления выходного напряжения. Эти параметры определяются по реакции ОУ на воздействие скачка напряжения на входе. [17]
Замеренные средние значения давлений оказывались, по-видимому, завышенными из-за воздействия почти прямого головного скачка уплотнения, периодически возникающего перед телом. [19]
Выше уже отмечалось, что при проектировании системы с конечным минимальным временем переходного процесса с нулевой установившейся ошибкой при воздействии скачка скорости реакция на единичную ступеньку получается неудовлетворительной. При этом время переходного процесса теоретически равно бесконечности. [20]
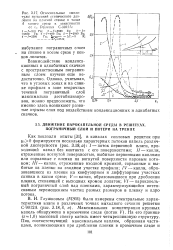 |
Относительные амплитуды пульсаций статического давления на плоской стенке в точке А косого среза в зависимости от Б.. Решетка С-9012 А. [21] |
Взаимодействие конденсационных и адиабатных скачков с пространственным пограничным слоем изучено еще недостаточно. Однако, учитывая, что в угловых зонах и на спинке профиля в зоне вторичных течений пограничный слой максимально дестабилизирован, можно предположить, что именно здесь возникают развитые отрывы слоя под воздействием конденсационных и адиабатных скачков. [22]
 |
Профили крыльев с острой передней кромкой. [23] |
Помимо перераспределения давлений, которое в итоге влияет на величины аэродинамических сил и моментов, действующих на самолет, при волновом кризисе нередко наблюдаются вибрации самолета. Они появляются вследствие двух причин: во-первых, скачок уплотнения, как правило, не стоит на одном месте, а непрерывно колеблется в продольном направлении, в связи с чем толчками изменяется величина аэродинамической силы крыла; во-вторых, при волновом кризисе наблюдается срыв потока с крыла, связанный с воздействием скачка уплотнения на пограничный слой. [24]
 |
Поле давлений во внешнем потоке. [25] |
Функции F и G выражаются уравнениями ( 13) и ( 28); ради упрощения мы снова приравняли нулю ширину скачка уплотнения. При х-со давление возмущения равно нулю. По мере изменения G оно экспоненциально растет до точки падения скачка уплотнения. Под воздействием скачка уплотнения давление возмущения растет вначале скачкообразно, а затем экспоненциально. [26]
Страницы: 1 2