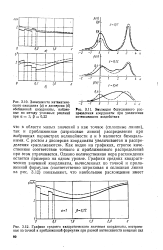
Дисперсия - координата
Cтраница 1
Дисперсии координаты и импульса одномерного квантового гармонич. [1]
Действительно, дисперсия координат центра тяжести при слабом сигнале увеличивается на величину, обратно пропорциональную суммарной энергии принимаемого сигнала и прямо пропорциональную средней квадратичной ширине пятна. Естественно, что все это остается справедливым и для р, если оценка проводится по центру тяжести. [2]
С ростом s дисперсия координаты увеличивается и распределения расплываются. Как видно на графиках, строгое качественное соответствие точного и приближенного распределений при этом утрачивается. Однако количественная мера расхождения остается примерно на одном уровне. [4]
Здесь Д) - дисперсия координаты L при отсутствии управлений; D ( - дисперсия координаты L с учетом действия радиотехнической системы управления; D0 / Di - отношение, характеризующее точность управления; ( - постоянная, характеризующая инерционные свойства объекта управления, рг2 / Г (, где Г; - постоянная времени объекта управления. [5]
Аналогичным образом можно проверить, что дисперсии координат и импульсов в когерентных состояниях не зависят от времени и, следовательно, минимизируют соотношение неопределенностей в произвольный момент времени. [6]
 |
Прямоугольная Н - U0 ( d ( x - a / 2 0 ( - а / 2 - х, потенциальная яма ( 144. [7] |
Таким образом, дисперсия импульса при свободном движении не изменяется, а квадрат дисперсии координаты при больших t растет квадратично со временем. Заметим, что состояние покоящейся частицы ( ( р) о 0) не является статическим, если д0р 0: соответствующий волновой пакет расплывается. [8]
Результаты § 4 позволяют находить оценки и доверительные интервалы для математических ожиданий и дисперсий координат случайного вектора, рассматриваемых по отдельности. Чтобы научиться оценивать ковариационную матрицу случайного вектора, оетается рассмотреть оценки ковариации. [9]
Здесь Д) - дисперсия координаты L при отсутствии управлений; D ( - дисперсия координаты L с учетом действия радиотехнической системы управления; D0 / Di - отношение, характеризующее точность управления; ( - постоянная, характеризующая инерционные свойства объекта управления, рг2 / Г (, где Г; - постоянная времени объекта управления. [10]
Таким образом, в случае оценки неизвестного векторного параметра 9 нижняя грань ( 17) дисперсии координаты Qp его несмещенной оценки 6 может быть больше нижней грани ( 8) дисперсии несмещенной оценки 6 параметра Ор в случае, когда 0 является единственным неизвестным скалярным параметром. Объясняется это тем, что во втором случае оценками могут служить функции результатов наблюдений U, зависящие от известных остальных координат вектора 9, вследствие чего класс допустимых оценок во втором случае шире, чем в первом. [11]
Соотношение неопределенностей, установленное Гейзенбергом и поэтому называемое соотношением неопределенностей Гейзенберга, выражает связь между дисперсией координаты и импульса частицы. [12]
Чтобы найти критерий для установления новой нумерации координат векторов, заметим, что доля первого фактора V в дисперсии р-й координаты вектора X равна отношению x p / kpp. [13]
Модель наблюдаемого случайного вектора Y, определяемая формулой ( 32) при выполнении условий 1) - 3), называется факторной моделью. Дисперсии координат вектора X, определяемого суммой в ( 32), называются факторными дисперсиями. [14]
Модель наблюдаемого случайного вектора У, определяемая формулой (10.32) при выполнении условий 1) - 3), называется факторной моделью. Дисперсии координат вектора X, определяемого суммой в (10.32), называются факторными дисперсиями. [15]
Страницы: 1 2