Дисперсия - совокупность
Cтраница 1
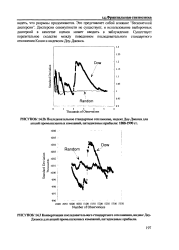 |
Конвергенция последовательного стандартного отклонения, индекс Доу-Джонса для акций промышленных компаний, пятидневные прибыли. [1] |
Дисперсии совокупности не существует, и использование выборочных дисперсий в качестве оценок может вводить в заблуждение. Существует поразительное сходство между поведением последовательного стандартного отклонения Коши и индексом Доу-Джонса. [2]
Известны ли дисперсии совокупностей, или же они оцениваются. [3]
Для характеристики средних определены дисперсии совокупностей. [4]
Он применяется в тех случаях, когда проверяемое распределение непрерывно и известны среднее и дисперсия совокупности. [5]
Таким образом, ( l / tt) ( sj s) является оценкой дисперсии совокупности данных, a s - - s называется полным разбросом внутри класса спроецированных выборок. [6]
В этом случае для проверки гипотезы необходимо воспользоваться формулой ( 191), так как дисперсия гене-ральной совокупности D ( Тн) известна. [7]
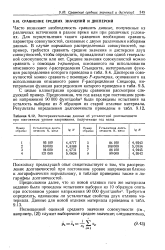 |
Экспериментальные данные об усталостной долговечности при постоянном уровне напряжения, полученные год назад. [8] |
Часто возникает необходимость сравнить данные, полученные из различных источников в разное время или при различных условиях. Для осуществления такого сравнения необходимо сравнить параметры совокупностей, связанные с двумя различными наборами данных. В случае нормально распределенных совокупностей, например, требуется сравнить средние значения и дисперсии двух совокупностей, чтобы определить, принадлежат они одной генеральной совокупности или нет. Средние значения совокупностей можно сравнить с помощью t - критерия, основанного на использовании описанного ранее - распределения Стьюдента, интегральная функция распределения которого приведена в табл. 9.4. Дисперсии совокупностей можно сравнить с помощью F-критерия, основанного на использовании описанного ранее F-распределения Снедкора, интегральная функция распределения которого приведена в табл. 9.5. С целью иллюстрации процедуры сравнения рассмотрим следующий пример. Предположим, что год назад при постоянном уровне напряжения 90 000 фунт / дюйм2 были проведены испытания на усталость выборки из 8 образцов из старой отливки материала. [9]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности, к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп ( Sharpe, 1963) говорил, что беты ( в смысле современной теории портфеля ( МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а 2 0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. [10]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности, к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп ( Sharpe, 1963) говорил, что беты ( в смысле современной теории портфеля ( МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а 2 0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. [11]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности, к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп ( Sharpe, 1963) говорил, что беты ( в смысле современной теории портфеля ( МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а 2 0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. [12]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности, к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп ( Sharpe, 1963) говорил, что беты ( в смысле современной теории портфеля ( МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а 2 0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. [13]
Для большинства индивидуумов, которые обучены стандартной гауссовой статистике, идея бесконечных среднего или дисперсии кажется абсурдной или даже извращенной. Еще раз повторим, что мы применяем частный случай, гауссову статистику, ко всем случаям. В этом случае математическое ожидание и дисперсия действительно существуют. Бесконечная дисперсия означает, что не существует дисперсии совокупности, к которой стремится распределение в пределе. Когда мы берем выборочную дисперсию, мы делаем это, согласно гауссову предположению, как оценку неизвестной дисперсии совокупности. Шарп ( Sharpe, 1963) говорил, что беты ( в смысле современной теории портфеля ( МРТ)) должны рассчитываться на основании ежемесячных данных за пять лет. Шарп выбрал пять лет, потому что этот период дает статистически значимую выборочную дисперсию, необходимую для оценки дисперсии совокупности. Пятилетний период статистически значим, только если лежащее в основе распределение является гауссовым. Если оно не является гауссовым и а 2 0, выборочная дисперсия ничего не говорит о дисперсии совокупности, потому что дисперсии совокупности нет. [14]
Страницы: 1