Диссоциированный воздух

Cтраница 1

Для диссоциированного воздуха в [82] представлена модель описания каталитических свойств поверхности силиконизированных теплозащитных покрытий, в которой особое внимание уделяется формированию молекул NO. Величины Са и А, характеризующие структуру поверхности для теплозащитных покрытий, основанных на SiO2, были выбраны примерно такимрг же, как и в предыдущих моделях. [1]

Для диссоциированного воздуха в [82] представлена модель описания каталитических свойств поверхности силиконизированных теплозащитных покрытий, в которой особое внимание уделяется формированию молекул NO. Величины Са и А, характеризующие структуру поверхности для теплозащитных покрытий, основанных на SiC2, были выбраны примерно такими же, и в предыдущих моделях. [2]

Давление в диссоциированном воздухе при температуре Т 4000 К уменьшается с 105 до 103 Па. Как изменяется его плотность. [3]

Например, в диссоциированном воздухе кислород содержится в атомарном и молекулярном видах, в окиси азота NO и в их ионах. [4]

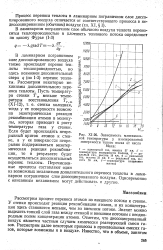Зависимость максимальной температуры у изолированной поверхности тупого носка от числа. [5]

В ламинарном пограничном слое диссоциированного воздуха также происходит перенос теплоты теплопроводностью, но здесь возможен дополнительный сверх q ( по 1 - 3) перенос теплоты. Рассмотрим некоторые механизмы дополнительного переноса теплоты. Если будет происходить непрерывный приток атомов к стенке, а у ее поверхности непрерывно поддерживаться экзотермическая реакция рекомбинации, то в результате будет осуществляться дополнительный перенос теплоты. [6]

В ламинарном пограничном слое диссоциированного воздуха также происходит перенос теплоты теплопроводностью, но здесь возможен дополнительный сверх q ( по 1.3) перенос теплоты. Рассмотрим некоторые механизмы дополнительного переноса теплоты. Тогда у ее поверхности возможна экзотермическая реакция рекомбинации ( соединения) атомов в моле-кулы, которая приводит к росту температуры газа у стенки. Если происходит непрерывный поток атомов к стенке, а у ее поверхности непрерывно поддерживается экзотермическая реакция рекомбинации, то в результате осуществляется дополнительный перенос теплоты. [7]

На каталитической поверхности в диссоциированном воздухе возможны различные химические процессы ( см. гл. В частности, атомы кислорода и азота могут адсорбироваться на активных местах поверхности, которые могут быть затем освобождены за счет миграционных процессов или термической десорбции. Они могут быть также вовлечены в рекомбинационные процессы в соответствии с механизмами рекомбинации Или-Райдила или Ленгмюра Хиншельвуда. Отметим, что в разреженном газе скачок между температурами поверхности и окружающей среды может быть значителен. Например, расчеты [133], проведенные для гиперболоида, моделирующего течение у Спейс Шаттла на высоте 92 35 км траектории второго полета, дают в точке торможения температуру в газе у поверхности около 1400 - 1500 К, в то время как температура поверхности только около 1000 К. В силу указанного скачка температуры сильно возбужденные и быстрые молекулы могут адсорбироваться диссоциативно, а при более сильном скачке температуры имеют место даже реакции диссоциации адсорбированных молекул. Если тепловая энергия в газовой фазе вблизи поверхности достаточно велика, то становится важным и диссоциативная адсорбция, обусловленная процессами, обратными реакциям Или-Райдила. В этом случае при ударе молекулы о поверхность возникают адсорбированный атом и атом в газовой фазе. Так как этот процесс сильно эндотермический, то он может произойти только в случае, когда температура в газовой фазе значительно выше той температуры поверхности, которая обычно наблюдается. В условиях режима с проскальзыванием, скачок температуры на поверхности может быть достаточно большим для осуществления этой реакции. Другим важным явлением, которое необходимо учитывать в этих условиях, является обсуждавшееся в предыдущем разделе явление неполной аккомодации химической энергии. [8]

На каталитической поверхности в диссоциированном воздухе возможны различные химические процессы ( см. гл. В частности, атомы кислорода и азота могут адсорбироваться на активных местах поверхности, которые могут быть затем освобождены за счет миграционных процессов или термической десорбции. Они могут быть также вовлечены в рекомбинационные процессы в соответствии с механизмами рекомбинации Или-Райдила или Ленгмюра-Хиншельвуда. Отметим, что в разреженном газе скачок между температурами поверхности и окружающей среды может быть значителен. Например, расчеты [133], проведенные для гиперболоида, моделирующего течение у Спейс Шаттла на высоте 92 35 км траектории второго полета, дают в точке торможения температуру в газе у поверхности около 1400 - 1500 К, в то время как температура поверхности только около 1000 К. В силу указанного скачка температуры сильно возбужденные и быстрые молекулы могут адсорбироваться диссоциативно, а при более сильном скачке температуры имеют место даже реакции диссоциации адсорбированных молекул. Если тепловая энергия в газовой фазе вблизи поверхности достаточно велика, то становится важным и диссоциативная адсорбция, обусловленная процессами, обратными реакциям Или-Райдила. В этом случае при ударе молекулы о поверхность возникают адсорбированный атом и атом в газовой фазе. Так как этот процесс сильно эндотермический, то он может произойти только в случае, когда температура в газовой фазе значительно выше той температуры поверхности, которая обычно наблюдается. В условиях режима с проскальзыванием, скачок температуры на поверхности может быть достаточно большим для осуществления этой реакции. Другим важным явлением, которое необходимо учитывать в этих условиях, является обсуждавшееся в предыдущем разделе явление неполной аккомодации химической энергии. [9]

Зависимость эффективного числа Прандтля для воздуха от температуры ( обозначения по. [10]

Система дифференциальных уравнений для течения диссоциированного воздуха в окрестности передней критической точки как в равновесном, так и в замороженном пограничном слое решена в работе [ 11, с. [11]

Система уравнений замороженного ламинарного пограничного слоя диссоциированного воздуха решена в работах [2, 11]; получены расчетные зависимости. Результаты расчета показали, что параметр теплообмена Nu / J / Re в замороженном пограничном слое на каталитической стенке ( например, металлической) мало отличается от соответствующей величины в равновесном пограничном слое; на не-каталитической стенке ( предположительно некоторые стекловидные материалы, окислы [56]) параметр теплообмена при некоторых условиях может стать меньше в два и более раз по сравнению с равновесным слоем. [12]

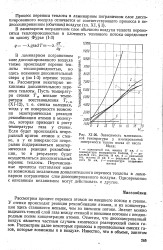Зависимость максимальной температуры у изолированной поверхности тупого носка от числа. [13]

Процесс переноса теплоты в ламинарном пограничном слое диссоциированного воздуха отличается от соответствующего процесса в недиссоциированном ( обычном) воздухе ( гл. [14]

Так в [36] показано, что при гиперзвуковом обтекании тела диссоциированным воздухом диффузионное разделение химического элемента кислорода существенно зависит от концентрации атомов на внешней границе пограничного слоя и от характера протекания гомогенных и гетерогенных каталитических реакций. Диффузионное разделение элементов на поверхности, обладающей свойством избирательности каталитического воздействия в отличие от случая идеально каталитической стенки, имеет место далее тогда, когда на внешней границе пограничного слоя присутствуют одни атомы. На химически нейтральной поверхности диффузионное разделение элементов может вызываться гомогенными химическими реакциями рекомбинации атомов кислорода и азота, если их константы скорости существенно различаются. В [117, 141, 142] установлено, что при исследовании обтекания каталитических поверхностей частично ионизованными смесями использование простых моделей диффузии приводит к существенным ошибкам при определении равновесной температуры поверхности и теплового потока к ней. Найдены режимы обтекания затупленных тел частично ионизованным газом, при которых конвективный тепловой поток к некаталитической стенке при постоянных концентрациях химических элементов более чем на 30 % больше, чем при правильном учете многокомпонентной диффузии. В [141, 142] предложена также простая модель описания диффузии, которая дает результаты, практически совпадающие с точными. [15]

Страницы: 1 2 3 4