Возможность - приближенное решение
Cтраница 1
Возможность приближенного решения плохо формализованной задачи определения области эффективности при многопараметрической многокритериальной оптимизации с использованием ЛПТ - поиска с усреднением определяется наличием предварительно выполненных аналитических исследований, быстродействием программ для моделирования и качеством обработки полученных результатов. [1]
Возможность приближенного решения рассматривалась Зйрингом и Поляньи [4], которые предложили способ, получивший название полуэмпирического метода вычисления энергии активации ( гл. Полная энергия связи двух атомов, например X и Y, определяется выражением А - - а. [2]
Возможность приближенного решения некорректной задачи основана на привлечении дополнительной информации о решении. В качестве независимых значений параметров mh, kh будем рассматривать значения этих параметров в прямоугольниках, в которых расположены скважины. Значения mh и kh для других прямоугольников определяются на основе одного из алгоритмов сглаживания - аппроксимация методом тренда, скользящее сглаживание, гармоническое сглаживание в результате решения уравнения Лапласа. [3]
Возможность приближенного решения вариационной задачи определяется тем, что существует последовательность конечномерных задач на стационарное значение, размерность которых стремится к бесконечности и решения которых сходятся к решению исходной задачи. Существование такой последовательности связано с сепарабельностью ( см. Приложение 1) пространства или, что эквивалентно, с наличием в нем счетной базы. [4]
Отсюда получается возможность приближенного решения сложных дифференциальных уравнений путем замены их соответствующим образом подобранными приближенными уравнениями, решающимися проще. Это обстоятельство может быть весьма существенно использовано уже при составлении дифференциального уравнения, отвечающего той или иной физической или технической задаче, между тем как при чисто математическом подходе это часто упускают из виду. [5]
Таким образом представление функции в виде ряда Фурье и возможность приближенного решения различных задач математической физики с помощью нескольких членов этого ряда оказываются следствием глубоких общих свойств самой задачи. [6]
При отображении (6.1) метод немедленно приводит к решению в замкнутом виде, а это предоставляет возможность приближенного решения задач указанного вида. [7]
Поэтому с практической точки зрения весьма важно установить закономерности, определяющие в ряде случаев характер распределения токов на поверхности тела и, следовательно, дающие возможность приближенного решения задач дифракции электромагнитных волн. [8]
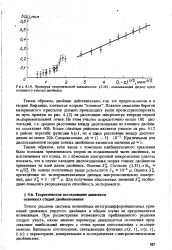 |
Проверка теоретической зависимости, описывающей форму пред-концевого участка двойника. [9] |
Точное решение системы нелинейных интегродифференциальных урав нений динамики упругого двойника в общем случае не представляется возможным. При рассмотрении возможности приближенного решения следует учесть, какие именно параметры движущегося скопления представляют наибольший интерес с точки зрения сопоставления с экспериментом. [10]
Следовательно, уравнение ( 23) при конечном значении обеспечивает только возможность вероятностных и приближенных решений. [11]
Если мы отбросим теперь силы внутреннего трения, оставив только силы инерции, то мы получим, очевидно, гидродинамику идеальной жидкости. Напротив, отбросив силы инерции и оставив силы трения, мы получаем возможность приближенного решения ряда задач о движениях вязкой жидкости. Целый ряд примеров такого Р ла разбирается нами в третьем разделе этой главы. [12]
Если мы отбросим теперь силы внутреннего трения, оставив только силы инерции, то мы получим, очевидно, гидродинамику идеальной жидкости. Напротив, отбросив силы инерции и оставив силы трения, мы получаем возможность приближенного решения ряда задач о движениях вязкой жидкости. Целый ряд примеров такого рода разбирается нами в третьем разделе этой главы. [13]
Доказывается, что вероятность u ( P) того, что точка, исходя из Р, впервые выходит из данной области G 3 ED P через фиксированную часть ее границы, удовлетворяет в пределе дифференциальному уравнению с частными производными эллиптического типа. Метод, который ведет к упомянутой выше предельной теореме теории вероятностей, позволяет доказать возможность приближенного решения классической задачи Дирихле с помощью уравнений в разностях. [14]
Страницы: 1