Динамическая возможность

Cтраница 1

Анализ динамических возможностей и энергетических характеристик привода является важным этапом процесса проектирования следящих систем, который следует проводить непосредственно после выявления технических требований к приводу. [1]

Условия динамической возможности движения абсолютно сжимаемой жидкости в форме Эйлера, полученные А. Фридманом, оказались очень полезными при решении различных задач гидродинамики абсолютно сжимаемой жидкости. Поэтому в настоящей работе мы устанавливаем эти условия и в форме Лагранжа; в то же время мы показываем, как можно приложить эти условия к решению частных задач гидродинамики абсолютно сжимаемой жидкости, задач, для которых форма Лагранжа представляет особые преимущества. [2]

Условиями динамической возможности движения вязкой жидкости пользуется Е.М. Золина в статье Ортогональное движение в атмосфере ( Геофизический сборник. В ортогональном движении скорости всех частиц параллельны между собою и перпендикулярны к направлению движущей силы. [3]

Движение, динамическая возможность которого интуитивно очевидна, мы будем иметь, предполагая, что соприкосновение происходит в вершине ( пересечение выпуклой поверхности твердого тела с осью тела) и что твердое тело равномерно вращается вокруг собственной оси ( направленной по восходящей вертикали), в силу чего центр тяжести G остается неподвижным, так же как и точка соприкосновения О. [4]

Аналогичным образом условия динамической возможности движения используют Б.И. Извеков, И.А. Кибель, Е.М. Золина в работах, которые будут изложены ниже. [5]

Приступая к исследованию динамических возможностей привода необходимо прежде всего найти величины скоростей и моментов на валу исполнительного двигателя, при которых обеспечивается требуемый закон движения выходного ( следящего) вала. [6]

Графический способ анализа динамических возможностей привода построением диаграммы нагрузки для ряда значений передаточного числа редуктора обладает наглядностью. Однако в большинстве случаев он сопряжен со значительной вычислительной работой. В связи с этим целесообразно, аппроксимируя границы области располагаемых моментов и скоростей отрезками прямых линий, получать в аналитическом виде необходимые условия обеспечения приводом требуемого закона движения следящего вала. Вид и число этих условий зависит от характера диаграммы нагрузки и области располагаемых моментов и скоростей. [7]

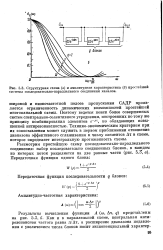Структурная схема ( а и амплитудная характеристика ( б простейшей системы последовательно-параллельного соединения каналов. [8]

САДР проявляется ограниченность динамических возможностей простейшей многоканальной схемы. Поэтому ведется поиск более совершенных систем спектрально-селективного усреднения, построенных по тому же принципу комбинирования элементов е-рг, но обладающих повышенной антирезонансностью. Технико-экономическим критерием при их сопоставлении может служить в первом приближении отношение диапазона эффективного сглаживания к числу элементов Ат в схеме, которое определяет интегральную протяженность схемы. [9]

Итак, условия динамической возможности движения сжимаемой жидкости состоят: 1) из условия незакручивае мости ( равенство ( а)), 2) из тепловых условий ( равенство ( Ь)) и 3) из объемных условий ( равенства ( с)), всего из пяти скалярных условий. Коль скоро условия эти выполнены, то Ф определится из равенств ( 19) до аддитивно входящей произвольной постоянной ( значит, со еф будет иметь множителем произвольную постоянную), а давление р определится из равенства ( 8) до аддитивно входящей произвольной функции времени. [10]

Итак, условия динамической возможности движения сжимаемой жидкости заключаются: 1) в условии незакручиваемости ( уравнение ( а)); 2) в тепловом условии ( уравнение ( Ь)) и 3) в условиях объема ( уравнение ( с)) - всего в пяти скалярных уравнениях. [11]

Переходя к условиям динамической возможности ортогонального движения сжимаемой жидкости, используем сначала условие незакручи-ваемости, которое должно выполняться и для нормальных движений и для полуконсервативных. [12]

В первой работе условия динамической возможности выводятся, исходя из уравнений гидродинамики в форме Лагранжа и результаты применяются к одному частному виду движения, часто встречающемуся в динамической метеорологии. [13]

Мы переходим к исследованию динамической возможности движения сжимаемой жидкости. [14]

В дальнейшем изучении условий динамической возможности нормального движения сжимаемой жидкости нужно различать два случая в зависимости от того, равен нулю или нет второй вектор. [15]

Страницы: 1 2 3 4