Возникновение - случайная погрешность
Cтраница 1
Возникновение случайных погрешностей неизбежно, поэтому в процессе измерений необходимо стремиться получать минимальные погрешности. Основной задачей теории точности измерений является установление общих правил расчетов и оценки точности измерений. [1]
В связи с тем, что возникновение случайных погрешностей неизбежно и неустранимо, основной задачей всякого процесса измерения является доведение погрешностей до минимума. [2]
Флуктуационные изменения влияющих величин приводят к возникновению случайной погрешности е, изменяющейся случайным образом при повторных измерениях одной и той же величины. [3]
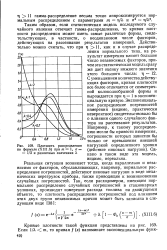 |
Плотность распределения. [4] |
Реальная ситуация возникает тогда, когда параллельно и независимо от факторов, обуславливающих, например, нормальное распределение погрешностей, действуют пиковые нагрузки в виде механических перегрузок прибора, также приводящие к возникновению случайных погрешностей. [5]
Случайные погрешности возникают обычно по ряду причин. Природа возникновения случайных погрешностей достоверно не всегда известна. Суммарное воздействие их, группируясь случайным образом, создает заметные погрешности различного знака. [6]
В практике использования средств измерений показания, полученные при многократном измерении одной и той же измеряемой величины, оказываются несовпадающими, даже в случаях, когда измерения выполняются одним и тем же прибором при неизменных условиях в ограниченном интервале времени. Очевидно, что причиной несовпадения результатов измерений является возникновение случайных погрешностей. Стандартизованным термином, характеризующим рассматриваемое свойство средств измерений, является сходимость показаний - качество средства измерений, отражающее близость к нулю его случайных погрешностей. [7]
При использовании на станке пневматической измерительной оснастки поток жидкости, попадающий в зону между торцом сопла и поверхностью пятки, может несколько исказить показания прибора. При врезном шлифовании, когда поток жидкости непрерывно омывает чувствительный элемент, это явление не приводит к возникновению случайной погрешности измерения. [8]
Вследствие возникновения случайных погрешностей при измерении, как бы тщательно оно ни было проведено, каждое повторное измерение приводит к новому числовому значению измеряемой величины. Однако при всей бессистемности в возникновении случайных погрешностей, они все же подчиняются определенным законам математической статистики, с помощью которых можно если не исключить случайные погрешности из результата измерений, то хотя бы оценить степень достоверности этого результата. Для проведения такой оценки необходимо произвести исследование достаточно большого ряда измерений одной и той же величины одним и тем же методом при неизменных условиях измерения. Поэтому получение надежного результата возможно, как правило, только при многократном повторении процесса измерения. [9]
Случайными называют погрешности, принимающие при повторных измерениях различные не связанные между собой положительные или отрицательные значения. Теория вероятностей называет случайным такое событие, которое при реализации данного комплекса условий может произойти или не произойти. Природа возникновения случайных погрешностей во многих случаях недостаточно ясна. Часто они возникают по ряду причин, суммарное воздействие которых, комбинируясь произвольно, создает заметные результирующие погрешности. Случайные погрешности нельзя, как систематические, исключить из результатов измерения. [10]
Случайными называют погрешности, принимающие при повторных измерениях различные взаимно несвязанные положительные или отрицательные значения. Теория вероятностей называет случайным такое событие, которое при реализации данного комплекса условий может произойти или не произойти. Природа возникновения случайных погрешностей во многих случаях недостаточно ясна. [11]
Случайными называют погрешности, величина и закономерности которых не определены. Случайность погрешности проявляется в том, что при многократном измерении одной и той же величины одним и тем же прибором с одинаковой тщательностью и в одинаковых окружающих условиях результаты измерений будут отличаться. Несмотря на бессистемность возникновения случайных погрешностей, они подчиняются законам теории вероятностей, с помощью которых можно оценить степень достоверности полученных результатов. [12]
Вследствие возникновения случайных погрешностей при измерении, как бы тщательно оно ни было проведено, каждое повторное измерение приводит к новому числовому значению измеряемой величины. Однако при всей бессистемности в возникновении случайных погрешностей, они все же подчиняются определенным законам математической статистики, с помощью которых можно если не исключить случайные погрешности из результата измерений, то хотя бы оценить степень достоверности этого результата. Для проведения такой оценки необходимо произвести исследование достаточно большого ряда измерений одной и той же величины одним и тем же методом при неизменных условиях измерения. Поэтому получение надежного результата возможно, как правило, только при многократном повторении процесса измерения. [13]
Требования высокой точности измерения температур заставляют осуществлять предварительное изучение факторов, вызывающих искажение нормальной работы как первичного преобразователя, так и средств накопления, хранения и переработки измерительной информации. Должна быть выявлена номенклатура таких влияющих факторов, характер и диапазоны их изменения, а также функции влияния каждого фактора на работу измерительной аппаратуры. Учет изменчивости влияющего фактора и его функции влияния позволяет определить частное детерминированное воздействие фактора на результат измерения, определить одну из составляющих возникающей систематической погрешности измерений. Случайные, нерегулярные колебания интенсивности влияющего фактора относительно принятой для него регулярной изменчивости вызовут возникновение частных случайных погрешностей. [14]
Страницы: 1