Возникновение - распределение
Cтраница 1
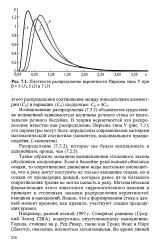 |
Плотности распределения вероятности Пирсона типа V при Р 3 ( 7 5 ( 2 и7 ( 5. [1] |
Возникновение распределения (7.3.2) объясняется существенно нелинейной зависимостью величины речного стока от влаго-запасов речного бассейна. [2]
Рассмотрим один типичный пример возникновения распределения - Пуассона. [3]
Рассмотрим один типичный пример возникновения распределения Пуассона. [4]
Математическая модель, ведущая к возникновению логнормаль-ного распределения, опирается на центральную предельную теорему, распространенную на случай зависимых величин. [5]
Гидрологи пока не могут объяснить физический механизм возникновения распределения Парето, и тем самым ответить на фундаментальный вопрос: почему катастрофические наводнения происходят так часто. В терминах оценки безопасности и риска хвост распределения соответствует так называемым гипотетическим наводнениям, возможность которых на практике пока не учитывается. Наличие степенного закона распределения вероятностей в корне изменяет наше представление о возможных масштабах бедствия. [6]
Гидрология пока не способна объяснить физический механизм возникновения распределения Парето и тем самым ответить на вопрос: почему катастрофические наводнения происходят так часто. Мною предложена простая феноменологическая динамическая модель колебаний стока, учитывающая водный баланс речного бассейна и нелинейную зависимость стока от влагозапасов. [7]
Однако случайные условия, которые должны сопутствовать возникновению распределения погрешности по закону Гаусса, зачастую нарушаются и могут возникать факторы, имеющие доминирующее значение. Рассмотрим влияние таких факторов с учетом различного характера их изменения во времени. [8]
Если внести изменения в условия, изложенные выше и сопутствующие возникновению распределения по закону Гаусса, и принять, например, что среди источников возникновения производственных погрешностей имеется фактор, резко выделяющийся ( доминирующий) среди всех остальных по оказываемому им влиянию на суммарную производственную погрешность ( при этом нару-шается третье из приведенных выше условий), то закон распределения суммарной погрешности будет в основном определяться законом распределения отклонений, вызванных доминирующим фактором. Каким ж е законам могут подчиняться доминирующие факторы. [9]
Распределения случайных величин, встречающиеся на практике в технических приложениях, нередко отличаются от своих теоретических прообразов, несмотря на то, что теоретическая схема возникновения распределения соответствует действительности, а количество практически наблюденных значений величины достаточно велико для того, чтобы имело смысл сопоставлять практические наблюдения с теоретическими. Часто встречающимися причинами этого является, например: 1) то, что практические данные относятся не ко всему распределению, а - к некоторой его части, полученной путем механического разделения исходного распределения, так называемые усеченные распределения, 2) то, что практические данные относятся к совокупности, образованной из нескольких механически объединенных вместе распределений ( по типу смешения нескольких партий изготовленных деталей), так называемые смешанные распределения. [10]
Новые бедные азотом участки, - которые IB результате обогащает. В этот процесс возникновения пятнистого распределения видов вносят свой вклад и травоядные животные. Они объедают траву на обширной площади, а азот, выделяемый с их пометом и мочой, концентрируется на небольших участках. Симбиотические бобовые растения в такой экосистеме определяют не только баланс азота, но и циклическое чередование видов в пятнисто организованном сообществе. [11]
Распределение по закону Гаусса было впервые подробно исследовано в конце XVIII и начале XIX века Гауссом применительно к ошибкам наблюдений и Лапласом при рассмотрении предельных распределений при повторении испытаний. Ляпунова, установивших условия возникновения распределения по закону Гаусса. Завершением этих работ явилась предельная теорема Ляпунова о распределении суммы независимых случайных слагаемых. [12]
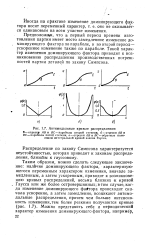 |
Антимодальные кривые распределения. [13] |
Предположим, что в первый период времени изготовления партии имеет место замедленное изменение доминирующего фактора по параболе, и во второй период - ускоренное изменение также по параболе. Такой характер изменения доминирующего фактора приводит к возникновению распределения производственных погрешностей партии деталей по закону Симпсона. [14]
 |
Монокристалл InSb, выращенный в обычных условиях. [15] |
Страницы: 1 2