Волна - плотность
Cтраница 1
Волна плотности в звездном диске представляет собой, по существу, - бароподобное искажение центральной области галактики, которая действует на газ. Положение резонансов определяется внутренней частью модели, в то время как инкремент нарастания зависит главным образом от плотности на внешнем резонансе. Уменьшение последней вызывает более медленный инкремент нарастания возмущений. [1]
Соответствующая осциллятору волна плотности вращается с угловой скоростью ( l / m) Qt Q2; т есть угловая периодичность волны, а I определяет радиальную структуру. [2]
В отличие от обычной волны плотности, TASS может при сжатии увеличивать плотность до 15 раз, существен но ускоряя процесс звездообразования. [4]
Эти условия соответствуют распространению волн плотности в жидкости с почти постоянной энтропией при совместном движении обеих жидкостей. [5]
Квазичастицы, соответствующие этим волнам плотности, носят названия плазмонов. Электронная плазма в металле отличается от обычной плазмы - сильно ионизированного газа - весьма большой концен трацией заряженных частиц. Такие энергичные плазмоны могут возникнуть в том случае, если, например, через металл пролетает быстрая заряженная частица с большой энергией. Hafpesa-нием металла таких плазмонов не создать, так как для этого нужны температуры, которых ни один металл не выдерживает. [6]
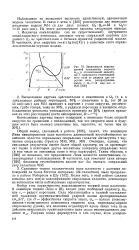 |
Зависимости невозмущенной компоненты скорости ахо и относительной амплитуды F спирального гравитационного поля от радиуса для коротких волн, распространяющихся с Qj, 16 км / с-кпс в МЗЗ. [7] |
Выбор этих характеристик подсказывается теорией волн плотности, В линейную теорию Линя и Шу входит один свободный ( параметр, lQpr или гс - радиус коротации. Сила образующейся в газовой составляющей галактики крупномасштабной ударной волны пропорциональна ( wJD) 2, где D - эффективная скорость звука, w - полная ( невозмущенная - ( - возмущенная) компонента скорости газа, перпендикулярная спиральному рукаву, эта величина осциллирует. [8]
Спиральную структуру принято рассматривать как волну плотности, распространяющуюся но галактич. Спирали могли возникнуть в результате развития гравитационной неустойчивости, когда силы тяготения в малом возмущении спиральной формы приводят к росту амплитуды возмущения. Возможны и др. причины возникновения спиралей. Такие неустойчивости, аналогично неустойчивостям плазмы, наз, кинетическими. [9]
Эта же неустойчивость должна приводить к крупномасштабным волнам плотности во вращающейся лабораторной плазме. Очевидно, что такой универсальной неустойчивостью, ответственной за динамику вращающейся сплошной среды, может быть какая-либо из гидродинамических неустойчивостей, вызванных наличием градиентов скорости и плотности в газовом диске плоской подсистемы спиральной галактики и во вращающейся лабораторной плазме. Использование в качестве экспериментальной среды жидкости или нейтрального газа не позволяет задавать нужные градиенты плотности скорости вращения, особенно при большом отношении величины разрыва скорости Ду к характерной скорости распространения возмущений в среде с. Возможность обсуждаемого плазменного эксперимента открывается благодаря тому, что, как доказано в работе [100], дисперсионные уравнения, описывающие колебания плазм-енной и гравитирующей сред, во многих интересных случаях аналогичны. [10]
Это напоминает смещение спирального узора в галактической волне плотности и может иметь важное значение для объяснения поведения секторного магнитного поля Солнца. [11]
Исходя из этого можно оценить абсолютную величину мощности шумовых волн плотности в условиях их максимального подавления и вблизи пускового режима, где их мощность максимальна. [12]
В [48] показано, что если в веществе устанавливается волна плотности с бесконечным набором характеристик волновых векторов ( что ассоциируется с неоднородным распределением свойств вещества в переходном дробно-размерном поверхностном слое), то вследствие флуктуационных эффектов всегда будет иметь место переход первого рода. [13]
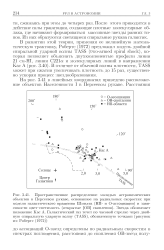
Изложенные выше принципы, классификации галактик, основанные на теории волн плотности, должны придать ей, по мнению авторов рассматриваемой работы [312], более объективный характер. Они отмечают удовлетворительную корреляцию между моделями галактик в предложенной классификации и типами Хаббла. [14]
В работе [100] рассматривается вопрос об аналогии между процессами образования спиральных рукавов галактик и волн плотности во вращающейся лабораторной плазме. Этот вопрос не нов: впервые на внешнее сходство фотографий спиральных рукавов галактик и плазменных сгустков в лабораторном эксперименте обратил внимание Бостик [169] около 20 лет тому назад. При инжекции плазменных сгустков из двух и более инжекторов в одну точку пространства снимок, сделанный в момент встречи этих сгустков, действительно очень напоминает снимки галактических спиралей. В экспериментах Бостика аналогия не простирается дальше чисто внешнего сходства в момент столкновения сгустков, каждый из которых Бостик отождествляет со спиральным рукавом. Таким образом, количество рукавов ( по Бостику) в точности равно количеству плазменных инжекторов - естественно, что такая аналогия не могла претендовать на серьезное обсуждение. Тем не менее, если обратиться к вопросу об аналогии между многообразием спиральных структур галактик и более скромных по размерам объектов, то среди последних прежде всего обращают на себя внимание вращающиеся массы газа и плазмы: хорошо известные фотографии. [15]
Страницы: 1 2 3 4 5