Регулярная волна
Cтраница 2
После окончания обработки опытов при нерегулярном волнении для возможности сопоставления величин орбитальных скоростей двухмерных нерегулярных и регулярных волн на той же установке с помощью тех же датчиков были проведены опыты с регулярными волнами. При этом параметры последних подбирались таким образом, чтобы период регулярных волн был равен среднему периоду нерегулярных волн, а высота регулярных волн была близка к максимальной высоте ( обеспеченностью около 1 %) нерегулярных волн. [16]
Наряду с традиционной концепцией расчета морских сооружений, основанной на анализе квазистатических нагрузок от регулярных волн ( детерминистический подход), в книге рассматриваются новые методы статических и динамических расчетов МНГС, базирующиеся на вероятностном подходе. Этот подход обусловлен случайным характером штормовых, волн и их воздействий на сооружения. Особое внимание обращено на необходимость учета конечной высоты волн различных типов ( регулярных, групповых и нерегулярных), что потребовало развития новых численных методов расчета, изложенных в этой книге. [17]
В § § 7, 8 речь идет о проблемах иного типа - о рассеянии регулярных волн в средах с хаотически изменяющимися параметрами. Это большая и быстро развивающаяся область статистической радиофизики и оптики. [18]
Следует отметить, что показанное теоретически П. Л. Капицей [31] являние возрастания массопередачи до 30 % при наличии регулярных волн подтверждается экспериментально. [19]
В заключение рассмотрим интересный для инженерной практики вопрос о соотношении квазистатических нагрузок на одиночные опоры при воздействии нерегулярных и регулярных волн. [20]
Стоячие волны, не перемещающиеся на поверхности воды по горизонтали, образуются при фронтальном подходе к вертикальной стене регулярных волн и глубинах, не меньших двойной высоты волны. [21]
В 1984 г. В. В. Яковлевым и А. В. Пятецким ( ИГМ АН УССР) была разработана новая численно-аналитическая методика расчета дифракции регулярных волн при их взаимодействии с препятствиями, имеющими форму тел вращений относительно вертикальной оси, в том числе с конусом и цилиндрической опорой с конической вставкой. [22]
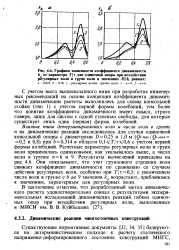 |
Графики зависимости коэффициента динамичности k от параметра Г / т для одиночной опоры при воздействии регулярных волн и групп волн и значениях - D / Л, равных. [23] |
В заключение отметим, что разработанный метод динамического расчета удовлетворительно совпал с результатами экспериментальных исследований динамических реакций гибких одиночных опор при воздействии регулярных волн, выполненных в МИСИ им. [24]
С помощью разработанного метода математического моделирования были выполнены численные исследования динамических реакций отдельно стоящей податливой круглоцшшндрической опоры как простейшего прототипа морского сооружения при воздействии регулярных волн и групп волн конечной высоты в глубоководной зоне. [25]
Зависимость (3.13), а также графики ( рис. 3.3 6) показывают, что в целом волновая нагрузка является достаточно сложной функцией времени г, параметров регулярных волн ( h, т, А. При этом скоростная составляющая qv удельной волновой нагрузки не является гармонической функцией, в то время как инерционная составляющая удельной волновой нагрузки q является гармонической функцией, причем скоростная и инерционная составляющие удельной нагрузки сдвинуты по фазе на 90 друг относительно друга. [26]
Исходя из принципа эквивалентности суммарной волновой нагрузки на сооружение, предлагается следующий порядок определения местоположения и величины эквивалентного диаметра D3 стоек пакета ( рис. 3.14, 3.15) на основе теории регулярных волн. [27]
После окончания обработки опытов при нерегулярном волнении для возможности сопоставления величин орбитальных скоростей двухмерных нерегулярных и регулярных волн на той же установке с помощью тех же датчиков были проведены опыты с регулярными волнами. При этом параметры последних подбирались таким образом, чтобы период регулярных волн был равен среднему периоду нерегулярных волн, а высота регулярных волн была близка к максимальной высоте ( обеспеченностью около 1 %) нерегулярных волн. [28]
Результаты сравнительного расчета силовых нагрузок на основе линейной модели нерегулярных волн по (5.68), занижают расчетные величины Raaa примерно на 20 % по сравнению с (5.1), (5.11), (5.12) нелинейной моделью расчета регулярных волн. [29]
В настоящей главе даны краткое описание физической природы ветровых волн и их классификация; кратко изложена методика определения параметров волн для инженерных расчетов, принятая в соответствующих нормативных документах; критически рассмотрены основные теории регулярных волн, групп волн и нерегулярных воли, описывающие кинематическую структуру волнового движения и пригодные для инженерных приложений, что позволило впервые сформулировать единый инженерный подход для расчета кинематики волн конечной высоты, как регулярных, так и групп волн и нерегулярных, выполнена оценка применимости различных теорий волн, в том числе и предлагаемого подхода, на основе данных экспериментальных исследований. [30]
Страницы: 1 2 3 4