Затухающая волна

Cтраница 2

В этом случае мы получаем затухающую волну. [16]

Теперь мы имеем дело с затухающей волной, амплитуда которой убывает по мере увеличения расстояния, пройденного волной в поглощающей среде. [17]

X было показано, что поля затухающих волн можно считать приближенно удовлетворяющими уравнению Лапласа. Это приближенно справедливое дифференциальное уравнение и является основой рассматриваемого в настоящем параграфе метода квазистационарного поля. Так как поля затухающих волн приближенно описываются уравнением Лапласа, строго справедливым для стационарных полей, то значит все известные методы расчета стационарных полей могут быть использованы для приближенного расчета поля затухающих волн. [18]

Решение уравнения ( Р) имеет характер затухающих волн. В практике это наиболее часто встречающийся случай. [19]

Авторы проанализировали полученное дисперсионное соотношение для случая затухающих волн и показали, что в области низких частот в слое существует одна сдвиговая волна, медленно затухающая при удалении от границы контакта слоя с упругим полупространством. С уменьшением длины волны переносимая этой волной энергия уменьшается и при длинах волн, меньших толщины слоя, появляется вторая затухающая вглубь волна с максимальным смещением на свободной поверхности пьезоэлектрика. В области высоких частот скорость распространения второй волны соответствует волне Гуляева-Блюстейна, что вполне объяснимо физически. [20]

Эти моды, очевидно, являются обобщениями затухающих волн, с которыми мы уже встречались ранее. [21]

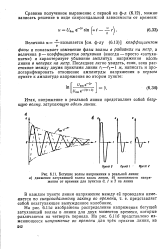Бегущие волны напряжения в реальной линии. а движение затухающей волны вдоль линии, б зависимости напряжения от времени для пунктов О, 1 и 2 на линии. [22]

На рис. 6.1 а изображено распределение напряжения бегущей затухающей волны в линии для двух моментов времени, которые различаются на четверть периода. [23]

Эти полосы непропускания характеризуются [372] нарастающими и затухающими волнами. [24]

Решение задачи в виде (6.28) указывает на существование затухающих волн с коэффициентом затухания, равным волновому числу. [25]

При ( от 1 снова становится возможным распространение слабо затухающих волн - так называемый нулевой звук. [26]

В случае прыжка-волны такое сечение располагается после ряда постепенно затухающих волн на значительном расстоянии от начала гидравлического прыжка, не позволяющем пренебрегать силами трения. [27]

Физическая причина этого кажущегося нефизического результата состоит в явлении затухающей волны. Следовательно, полностью некогерентный поверхностный источник не излучает. [28]

Если вычесть (3.2.62) из (3.2.61), то вклады от затухающих волн сокращаются. [29]

При и) т 1 снова становится возможным распространение слабо затухающих волн - так называемый нулевой звук. [30]

Страницы: 1 2 3 4