Гравитационно-капиллярная волна
Cтраница 1
Зависимость групповой скорости гравитационно-капиллярных волн от длины волны приведена на рис. 10.9. Из теории волн бесконечно малой амплитуды следует экспоненциальное убывание с глубиной скорости движения частиц в волне, круговые траектории движения частиц при волновом движении, экспоненциальное убывание с глубиной радиуса этих окружностей. При этом затухание волн с глубиной происходит избирательно: короткие волны затухают быстрее, чем длинные. [1]
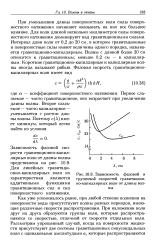 |
Зависимость фазовой и групповой скоростей гравитационно-капиллярных волн от длины волны. [2] |
Зависимость фазовой скорости гравитационно-капиллярных волн от длины волны представлена на рис. 10.9. Для линейных гравитационно-капиллярных волн их характеристики являются аддитивными функциями гравитационных сил и сил поверхностного натяжения. [3]
Зависимость групповой скорости гравитационно-капиллярных волн от длины волны приведена на рис. 10.9. Из теории волн бесконечно малой амплитуды следует экспоненциальное убывание с глубиной скорости движения частиц в волне, круговые траектории движения частиц при волновом движении, экспоненциальное убывание с глубиной радиуса этих окружностей. При этом затухание волн с глубиной происходит избирательно: короткие волны затухают быстрее, чем длинные. [4]
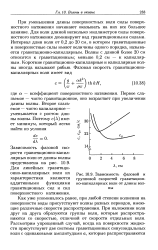 |
Зависимость фазовой и групповой скоростей гравитационно-капиллярных волн от длины волны. [5] |
Зависимость фазовой скорости гравитационно-капиллярных волн от длины волны представлена на рис. 10.9. Для линейных гравитационно-капиллярных волн их характеристики являются аддитивными функциями гравитационных сил и сил поверхностного натяжения. [6]
Выражение (3.77) соответствует дисперсионному уравнению гравитационно-капиллярных волн. [7]
Оказывается, что уравнения Буссинеска справедливы не только для гравитационно-капиллярных волн; аналогичные уравнения можно получить и для других типов волн, в частности для волн в плазме. [8]
На спектре хорошо прослеживаются волновые колебания разных масштабов и периодов: область капиллярных и гравитационно-капиллярных волн, ветровые волны, зыбь, длинные гравитационные волны и цунами, приливные волновые периоды, инерционные периоды и планетарные волны. [9]
Зависимость фазовой скорости гравитационно-капиллярных волн от длины волны представлена на рис. 10.9. Для линейных гравитационно-капиллярных волн их характеристики являются аддитивными функциями гравитационных сил и сил поверхностного натяжения. [10]
Ма является комбинацией модулей, соответствующих простым типам деформации. Введенный модуль Мд, который соответствует распространению поверхностных гравитационно-капиллярных волн, будем использовать без расшифровки, имея в виду, что он может оказаться сложным. [11]
Мп является комбинацией модулей, соответствующих простым типам деформации. Введенный модуль Ма, который соответствует распространению поверхностных гравитационно-капиллярных волн, будем использовать без расшифровки, имея в виду, что он может оказаться сложным. [12]
Получающиеся при этом граничные условия для скорости (5.11) позволяют получить простое точное решение задачи. Эти граничные условия, однако, являются в известной степени искусственными. В действительности свободная поверхность под действием возмущений деформируется. Поэтому следует, строготоворя, учитывать, что возникновение конвективных возмущений в жидкости приводит к искривлению свободной поверхности и появлению на ней гравитационно-капиллярных волн. [13]
Страницы: 1