Дифрагированная волна

Cтраница 4

Если за кристаллом размещен анализатор, то амплитуда дифрагированной волны может быть получена умножением (7.41) на матрицу Джонса анализатора, приведенную к системе координат, оси которой совпадают с направлениями поляризации собственных световых мод в кристалле. После этого может быть вычислена дифракционная эффективность. [46]

Между тем, знание законов возбуждения и распространения дифрагированных волн позволяет решить ряд задач ультразвукового контроля, которые обычными методами контроля решить крайне сложно либо вообще нельзя. К ним можно отнести распознавание типа дефекта и измерение его размеров, выявление сигналов на фоне шума в некоторых сварных швах, измерение глубины закаленных слоев и др. В табл. 1.4 приведены некоторые схемы контроля с использованием волн дифракции. [47]

Выясним, каким видом разложения в ряд эйконала дифрагированной волны Фт предпочтительно пользоваться в дальнейшем. [48]

Пространственная несимметрия наклонных диафрагм обусловливает несовпадение амплитуд высших дифрагированных волн одинаковых номеров при падении Я о-волны с той или иной стороны структуры. [49]

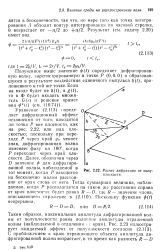Расчет дифракции от полуплоскости. [50]

Полученное выше значение p ( t) определяет дифрагированную волну, зарегистрированную в точке Р ( 0 0 0) и образовавшуюся в результате воздействия единичного импульса 6 ( 0 приложенного к той же точке. [51]

Конкретная дифракционная задача приобретает замечательную простоту, если дифрагированную волну записать в виде суммы плоских волн с различными амплитудами, а направляющие косинусы выбрать в качестве параметров. [52]

ЗХ в которой потенциал ср представляет собой потенциал одной дифрагированной волны. [53]

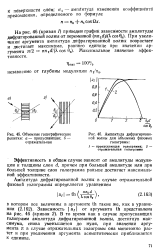Амплитуда дифрагированной волны для объемных фазовых голограмм. [54]

В то время как в случае пропускающих голограмм амплитуда дифрагированной волны, достигнув максимума, снова уменьшается до нуля, при значении аргумента я в случае отражательных голограмм она монотонно растет и при увеличении аргумента асимптотически приближается к единице. [55]

Согласно уравнению ( 7), существует бесконечная совокупность дифрагированных волн, непрерывно распределенных по углу. [56]

Если это условие выполняется, то из кристалла будет выходить дифрагированная волна, соответствующая отражению от атомных плоскостей, определяемых вектором gi и нормальных к этому вектору. [57]

Применение обоих видов разложения к формуле (1.13) показывает, что дифрагированная волна, как и падающая, в первом приближении будет сферической. [58]

Схемы определения кинематических характеристик ударной волны методом светящихся зазоров ( а и методом клина ( б. Справа показаны щелевые фоторегистрограммы. [59]

В результате обработки растровых фоторегистраций было установлено, что вдоль дифрагированной волны радиус кривизны детонационного фронта уменьшается и на границе темной зоны ( линии прекращения детонации) достигает своего минимума, по величине близкого к значению критического радиуса кривизны RKp (3.22), зависящего от толщины слоя ВВ и его детонационной способности. При кривизне фронта детонационной волны меньшей RKp детонация затухает. [60]

Страницы: 1 2 3 4