Нестационарная волна

Cтраница 2

ТНТ, гексогена и октогена с добавками до 30 % А1, показало, что время реакции алюминия за фронтом ДВ - т, варьируемое в диапазоне от 0 1 мкс до т - ос, не влияет на параметры фронта этих смесевых ВВ, а изменяет лишь пространственно-временное распределение параметров ПД за фронтом в нестационарной волне разгрузки. Такое влияние добавки А1 и времени его догорания г определяются особенностями расположения ударных адиабат ( адиабат Гюгонио) и изоэнтроп расширения равновесных ( с конденсированным окислом А ОЗ) и частично неравновесных ( с инертным ударно сжатым во фронте ДВ алюминием) продуктов детонации на ( р-г) - плоскости. [16]

Нестационарные возмущения в линейной теории можно представить ( используя интегралы Фурье) в виде суперпозиции синусоидальных волн. Примером исследования геометрической дисперсии нестационарных волн, основанного на разложениях Фурье, является работа Пека и Гертмана [55], в которой проведен анализ распространения нестационарных волн в направлении слоев в среде показанного на рис. 2 вида. [17]

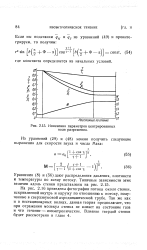Изменения параметров центрированных волн разрежения. [18]

На рис. 2.16 приведены фотографии потока около стенки, искривленной внутрь и наружу по отношению к потоку, полученные в сверхзвуковой аэродинамической трубе. Так же как и в нестационарных волнах, данная теория предполагает, что при отражении молекул стенка не влияет на состояние газа и что течение - изоэнтропическое. [19]

Таким образом, при Da С / Се реализуется первый случаи, который соответствует стационарной ударной волне, имеющей впереди себя стационарный скачок, а при С D0 Cf Сй - BTopoii случай, когда интегральная кривая дает непрерывное распределение параметров в стационарной ударной волне сжатия. Это решение есть предел, к которому при сохранении интенсивности источника возмущения стремится нестационарная волна с постепенно ослабляющимся и стремящимся к нулевой интенсивности передним скачком. [20]

Таким образом, при Da С; Се реализуется первый случай, который соответствует стационарной ударной волне, имеющей впереди себя стационарный скачок, а при Се D0 Cf - Cg - второй случай, когда интегральная кривая дает непрерывное распределение параметров в стационарной ударной волне сжатия. Это решение есть предел, к которому при сохранении интенсивности источника возмущения стремится нестационарная волна с постепенно ослабляющимся и стремящимся к нулевой интенсивности передним скачком. [21]

Для того чтобы асимптотическое выражение (2.5), из которого вытекают все эти результаты, было достаточно точным, необходимо, чтобы k ( x, t) и со ( л, t), a также W ( x, t) изменялись достаточно мало на расстояниях порядка длины волны 2n / k и за промежутки времени порядка 2тс / со. Поэтому все эти результаты можно было бы получить также методом геометрической оптики [14], представляя нашу нестационарную волну в виде (2.16), где а ( х, t) - медленно меняющаяся амплитуда, а эйконал 6 ( х, t) - большая величина. [22]

В заключение коснемся работы Хегемира [52], в которой детально изучались стационарные и нестационарные колебания в слоистых и волокнистых композитах. В этой работе основное внимание уделяется анализу явлений рассеяния в упругих материалах, однако приводится и решение для нестационарных волн в вязкоупругих слоистых композитах, распространяющихся перпендикулярно слоям. Это решение было получено при помощи принципа соответствия и обращения преобразования Лапласа. [23]

По американским данным, новая схема организации взрывных работ может обеспечить уменьшение стоимости горнодобычи примерно на 10 % и в масштабах страны дать экономию более чем в 250 млн. долларов в год. Точные количественные оценки требуют углубленного исследования динамической прочности и трещиностойкости горных пород при высоко-1 скоростном нагружении, решения сложных нелинейных динамических задач о распространении нестационарных волн большой амплитуды. Однако огромные выгоды, которые сулит математическая теория оптимального взрыва твердых тел, безусловно, стимулируют работу ученых-механиков в этом направлении. [25]

Однако вытекающие из законов сохранения массы, количества движения и энергии уравнения вместе с уравнением состояния недостаточны для определения скорости детонации D, поскольку эти уравнения содержат четыре неизвестных величины рс, vr, Тг и D, тогда как из законов сохранения и уравнения состояния могут быть получены лишь три неизвестных. Каждая частица газа в детонационной волне претерпевает следующие превращения. Далее, в результате реакции давление и объем газа меняются вдоль касательной по направлению от точки p v к точке К, в которой необратимые химические реакции заканчиваются. Дальнейшее расширение газа происходит изоэнтропически в нестационарной волне разрежения. [26]

В настоящей главе была сделана попытка дать сводку результатов, полученных в различных экспериментальных и теоретических работах по волнам и колебаниям, возникающим в направленно армированных композитах, для случая малых деформаций и линейных определяющих уравнений. Эта попытка представляется своевременной, так как за последние годы достигнуты значительные успехи в понимании особенностей линейного динамического поведения композиционных материалов. Линейная теория с ее точными результатами для слоистой среды и различными хорошо обоснованными приближенными подходами к описанию как слоистых, так и волокнистых композитов в настоящее время близка к полному завершению. Этот объем теоретических сведений дополняется экспериментальной проверкой результатов, относящихся к распространению сину-соида льных волн и импульсных возмущений. Следует отметить, однако, что необходимость проведения дальнейших экспериментальных исследований все еще остается важной. Многое еще предстоит сделать и в решении задач с нестационарными волнами, в особенности в определении локальных значений полевых переменных, таких, как напряжения на поверхности раздела фаз и динамическая концентрация напряжений. [27]

Страницы: 1 2