Параметрическая волна
Cтраница 1
Порог возбуждения параметрических волн впервые определен в [5], где учет вязкости произведен феноменологически, путем подстановки демпфирующего слагаемого в уравнение Матье, описывающее поведение поверхности невязкой жидкости при наличии вертикальных вибраций. [1]
Условия возбуждения параметрических волн были получены в § 1.1 для равновесной в отсутствие вибраций ситуации, когда легкая жидкость расположена поверх тяжелой. Полученные там формулы легко переписать для инверсного расположения жидкостей. [2]
В отличие от ряби Фарадея, возбуждение параметрических волн горизонтальными вибрациями изучено сравнительно слабо. В работе [32] исследовалась устойчивость плоской поверхности раздела двух осциллирующих потоков, разность скоростей которых является периодической функцией времени. Рассмотрение было проведено в рамках модели идеальной жидкости для бесконечно толстых слоев жидкостей. [3]
Между тем, вязкость играет важную роль в формировании параметрических волн. Именно ею определяется порог возбуждения параметрического резонанса. Кроме того, как будет показано ниже, решения нелинейной задачи о параметрических волнах, полученные без последовательного учета вязкости, расходятся в коротковолновой части спектра. Отметим еще, что, как показано В.Е. Захаровым [26], для капиллярно-гравитационных волн на поверхности идеальной жидкости вообще нет устойчивых решений. В настоящем параграфе нелинейная теория параметрически возбуждаемых волн строится на основе уравнений движения и соответствующих граничных условий для вязкой жидкости. [4]
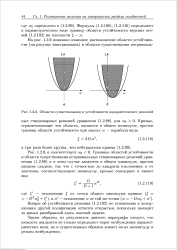 |
Области существования и устойчивости надкритических решений. [5] |
Таким образом, из результатов данного параграфа следует, что вязкость жидкости не только определяет порог возбуждения параметрических волн, но и существенным образом влияет на их амплитуду и режим возбуждения. [6]
Линейная теория позволяет определить лишь порог возбуждения ряби Фарадея. Вопрос об амплитуде и режиме возбуждения параметрических волн требует учета нелинейных эффектов. [7]
Между тем, вязкость играет важную роль в формировании параметрических волн. Именно ею определяется порог возбуждения параметрического резонанса. Кроме того, как будет показано ниже, решения нелинейной задачи о параметрических волнах, полученные без последовательного учета вязкости, расходятся в коротковолновой части спектра. Отметим еще, что, как показано В.Е. Захаровым [26], для капиллярно-гравитационных волн на поверхности идеальной жидкости вообще нет устойчивых решений. В настоящем параграфе нелинейная теория параметрически возбуждаемых волн строится на основе уравнений движения и соответствующих граничных условий для вязкой жидкости. [8]
Страницы: 1