Сорбционная волна

Cтраница 1

Стационарный фронт сорбционной волны, перемещающийся с постоянной скоростью, начинает формироваться во втором аппарате каскада. Однако при нагрузках по жидкой фазе более 100 м3 рассола на 1 м3 ионита в 1 ч одновременно с ростом скорости массопереноса происходит резкое снижение обменной емкости ионита по иоду, вызванное уменьшением времени контакта взаимодействующих фаз [ 103, с. Оказывается, что технологически целесообразней более полное насыщение ионита нежели более высокая скорость массопереноса, поскольку это обеспечивает высокие технологические показатели на последующих стадиях процесса. [1]

Наличие конечного фронта сорбционной волны позволяет разбить весь процесс на две стадии. [2]

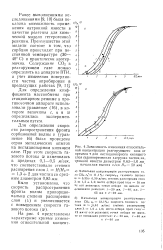
Динамические кривые распределения меченого иона иттрия в колонке Са-обменной смолы. [3]

Теоретический профиль фронта сорбционной волны был рассчитан по формуле ( 17) для момента F 95 мл. [4]

Теоретический профиль фронта сорбционной волны, рассчитанной яо формуле ( 18) для момента V 95 мл, на рис. 5 указан пунктиром. [5]

Прогрев сорбента впереди фро-нта сорбционной волны в этом случае осуществляется за счет теплопроводности, вследствие чего зона поглощения увеличивается. [6]

Эта точка называется центром тяжести сорбционной волны. [7]

Зависимость изменения относительной концентрации реагирующего газа от времени т для нестационарного кипящего слоя ( единовременная загрузка частиц на. тронной извести диаметром 0 63 - 1 0 лш начальная высота елся Но 50 мм. [8]

Для определения скорости распространения фронта сорбционной волны v ( уравнение 16) была проведена серия методических опытов на нестационарном кипящем слое. [9]

Он показал, что скорости движения отдельных сорбционных волн по своим величинам располагаются в порядке, обратном относительной сорбируемости компонентов смеси. При этом каждая отдельная волна распространяется со скоростью, большей той, с которой распространялось бы каждое отдельное вещество при той же входной концентрации. В этом процессе проявляется десорбирующее действие сильнее сорбирующегося компонента смеси. Для случая динамики сорбции двух веществ, сорбция которых подчиняется изотерме Ленгмюра, даны количественные закономерности процесса, выведены формулы скоростей движения фронтов, а также формулы для определения концентраций компонентов в зонах. Для более сложных систем дано решение в общей форме. Тизелиус [77, 228], независимо от О. М. Тодеса [139], дали расчетные формулы для определения концентраций веществ в зонах первичной, фронтальной хроматограммы и на этой основе разработали экспериментальный метод хроматографического анализа смесей веществ, получивший название фронтального анализа. [10]

Лангмюра, интерполяционная 107 Фронт адсорбционного возмущения ( сорбционной волны) 37 ел. [11]

В работе предлагается графоаналитический метод вычисления Дсср для случая образования стационарного фронта сорбционной волны по изотерме сорбции. [12]

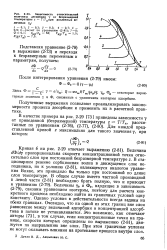Зависимость относительной величины десорбции v от безразмерной температуры z Т / Ткпри различных ве. [13]

Величина пропорциональна скорости концентрационной точки относительно слоя при постоянной безразмерной температуре г. В стационарном режиме сорбционная волна в движущемся слое неподвижна, но к условию ( 2 - 81), являющемуся аналогом уравнения Викке, это приводило бы только при постоянной по длине слоя температуре. Величины у0 и Ф0, входящие в зависимость ( 2 - 79), связаны уравнением изотермы, поэтому для расчета конкретного процесса необходимо найти из граничных условий одну константу. Однако условия в действительности всегда заданы на обеих границах. Очевидно, что на одной из этих границ вне слоя равновесие между величиной адсорбции и концентрацией адсорб-тива в потоке не устанавливается. Это возможно, как отмечают авторы [73], в том случае, если концентрационные точки на границе, скорости которых определены по выражению ( 2 - 81), движутся по направлению вне слоя. При этом граничные условия не могут оказывать влияния на протекание процесса внутри слоя. [14]

Как показано в работе О. М. Тодеса и Ю. С. Левина [7], характер процесса зависит от соотношения скоростей изотермической сорбционной волны v и волны прогрева ( охлаждения) w, а также вида изотермы. [15]

Страницы: 1 2