Сферическая волна
Cтраница 2
Упруго-пластическая сферическая волна иагружения, Прикл. [16]
Сферическая волна электрического тока (2.56) является безвихревой и, как это отмечалось в § 1.3, не создает полей излучения. Поэтому нужно учесть два основных фактора, нарушающих эту симметрию и приводящих к возникновению вихревых сторонних токов. [17]
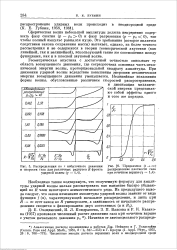 |
Распределения по г избыточного давления. [18] |
Сферическая волна небольшой амплитуды должна непременно содержать фазу сжатия ( р - р0 0) и фазу разрежения ( р - р0; 0), так чтобы полный импульс равнялся нулю. Это требование ( которое является следствием закона сохранения массы) вытекает, однако, из более точного-рассмотрения и не содержится в теории геометрической акустики ( как линейной, так и нелинейной), использующей такие же соотношения между функциями, как и в плоской звуковой волне. [19]
Пусть сферическая волна инициирована на радиусе R и движется внутрь, а продукты взрыва свободно разлетаются наружу. [20]
Эйконал сферической волны, сходящейся в точку, отличается от эйконала расходящейся волны только знаком. [21]
Фронт сферической волны представляет собой сферу, в центре которой находится источник колебаний, а звуковые лучи совпадают с радиусами сферы. [22]
У сферических волн волновые поверхности представляют собой систему концентрических сфер, центры которых расположены в одной точке - фокусе волн. Их можно получить, например, от источника волн, представляющего собой маленький пульсирующий шарик. Так как шарик имеет конечные размеры, то каждая точка его пульсирующей поверхности является, по существу, точечным источником волн, наложение которых и дает действительную волну. Однако на расстоянии, много большем диаметра шарика, этим можно пренебречь и образующиеся волны рассматривать как сферические. При этом условии сам шарик принимают за точечный источник волн. [23]
Примером сферических волн являются звуковые волны, возбуждаемые колеблющимися телами, размеры которых достаточно малы. [24]
Примером сферических волн могут служить волны, возникающие в воздухе вокруг маленького изотропного источника звука, например, вокруг маленького колокольчика. [25]
Амплитуда сферической волны пропорциональна произведению амплитуды поля распространяющегося в среде излучения на флуктуирующую часть показателя преломления п ( г а фаза определяется общим числом длин волн, укладывающихся на пути от источника до рассеивателя и далее до приемника. [26]
Отражение сферической волны от границы раздела между двумя средами представляет особый интерес ввиду того, что оно может сопровождаться своеобразным явлением возникновения боковой волны. [27]
Система сферических волн имеет свои преимущества для описания картины, наблюдаемой из данной точки, которую удобно принять за начало координат. [28]
Отражение сферической волны от границы раздела между двумя средами представляет особый интерес ввиду того, что оно может сопровождаться своеобразным явлением возникновения боковой волны. [29]
Амплитуды сферических волн в R3, описывающих процессы захвата частиц, определены в терминах компонент Г - мат - РИЦЕ. Отметим, что, когда потенциалы Va ( x) убывают быстрее любой степени Ы - г, асимптотические слагаемые младшего порядка для этих функций можно задать, с помощью рекуррентных соотношений. Уравнение Шредингера будет выполняться при этом с точностью до произвольной степени Ы - г. Такие рекуррентные соотношения будут приведены в § 1 следующей главы. [30]
Страницы: 1 2 3 4