Двухслойный волновод
Cтраница 2
Рассмотрим дифракцию волны Ни круглого волновода на диэлектрическом стержне конечной длины L. На рис. 1.22 представлены дисперсионные кривые волн низших типов двухслойного волновода, образованного металлическим экраном и диэлектрическим стержнем. [16]
Исследование его оператора производится так же, как и круглого двухслойного волновода. Лишь для волн Egm, Щт краевые задачи являются самосопряженными. Все гибридные волны описываются несамосопряженными операторами. Введение между слоями резистивной пленки делает краевую задачу, решаемую с помощью МПТ, для всех волн несамосопряженной. Таким образом определили типы краевых задач для всех направляющих структур, которые будут рассматриваться ниже, и тем самым предварительно ответили на вопрос: какие спектры волн соответствуют этим структурам. [17]
 |
Характеристики двухслойных круглого и эллиптического волноводов с резистивиыми пленками. [18] |
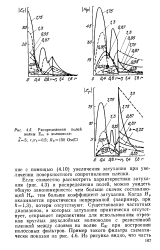
На рис. 4.13 представлены дисперсионные характеристики и характеристики затухания волн НЕц и ЕНц двухслойного круглого волновода и волны HE j двухслойного эллиптического волновода при одинаковых е и / У / 2, где гЬ2 - радиусы внутреннего слоя и экрана в круглом и большие полуоси внутреннего слоя и экрана в эллиптическом волноводах. Волны НЕц в обычных круглом и НЕ4) в эллиптическом двухслойных волноводах схожи по структуре полей и по дисперсионным зависимостям. Сходство сохраняется и при введении в волноводы резистивных пленок. Волны НЕП в круглом и НЕ ] 1, в эллиптическом волноводах с пленками имеют критические частоты. При этом решения дисперсионных уравнений на частотах выше критических всегда лежат в первых квадрантах плоскостей ( xi 2); ниже критической - в четвертых квадрантах этих плоскостей. При переходе через критическую частоту, на которой-р Р 0, фазовая скорость меняет знак. На частотах выше критической указанные волны в обоих волноводах могут быть и быстрыми, и медленными. [19]
Классификация волн в двухслойном круглом экранированном волноводе с резистивной пленкой производится на основе предельного перехода ( Дсг - - 0) к обычному двухслойному волноводу. Нетрудно видеть, что уравнение (4.4) при Дсг 0 превращается в дисперсионное уравнение двухслойного волновода без резистивной пленки ( см. гл. В связи с этим при поиске решений уравнения (4.4) в качестве отправных точек целесообразно брать решения этого уравнения при Асг 0, а затем, постепенно увеличивая параметр Дсг, получать из (4.4) волновые числа собственных волн волновода с резистивной пленкой. [20]
Эти условия определяют частотный диапазон, в котором существуют комплексные волны в слоистых волноводах без потерь. Как известно [23], границам указанного диапазона соответствуют точки жордановой кратности 2-го порядка на дисперсионных кривых собственных волн. Из этого условия для двухслойного волновода несложно получить трансцендентное уравнение, которое совместно с дисперсионным уравнением (1.9) позволяет при фиксированных параметрах волновода е и ajb рассчитывать границы частотного диапазона существования комплексных волн и соответствующие им значения постоянной распространения. [21]
Но в этом случае критическая частота волны в волноводе с пленкой должна совпадать с ( Окр той же волны в волноводе без пленки. Действительно, критические частоты волны HEJ1, в обоих волноводах совпадают. Таким образом, для круглого и эллиптического двухслойных волноводов с резистивными пленками обнаруживаем общую закономерность: волны HEU и HEj1, имеют критические частоты ( причем они совпадают с критическими частотами этих волн в волноводе без пленки), волны EHtl и ЕН, [ критических частот не имеют. [22]
 |
Распределения полей волны EOI в волноводе. [23] |
Если совместно рассмотреть характеристики затухания ( рис. 4.3) и распределения полей, можно увидеть общую закономерность: чем больше скачок составляющей Hv, тем больше коэффициент затухания. Когда Я9 оказывается практически непрерывной ( например, при k 1 3), потери отсутствуют. Существование частотных диапазонов, в которых затухание практически отсутствует, открывает перспективы для использования отрезков круглых двухслойных волноводов с резистивной пленкой между слоями на волне Е0 при построении полосовых фильтров. [24]
 |
Характеристики волны EOI при. 5. п / г20 5. [25] |
На рис. 4.3 представлены результаты решения дисперсионного уравнения (4.8) для волны E0i при различных значениях поверхностного сопротивления пленки. Численные расчеты подтверждают отсутствие у симметричной Е - волны критических частот. При достаточно больших поверхностных сопротивлениях пленки, как видно из рис. 4.3, дисперсионные характеристики, начиная с некоторой частоты, проходят вблизи диспер-синной характеристики обычного двухслойного волновода с теми же параметрами. На рис. 4.3 она изображена штриховой линией. Сближение характеристик, как правило, начинается на частотах, немного превышающих критическую частоту волны E0i обычного двухслойного волновода. [26]
Как видно из рис. 4.3, с ростом частоты фазовая постоянная увеличивается, что легко объясняется с помощью формулы (3.29), обобщающей закон сохранения энергии. Однако при определенных параметрах пленки в поведении дисперсионных характеристик наблюдается немонотонность: в отдельных участках диапазона фазовая постоянная с ростом частоты может уменьшаться. Поскольку в волноводе с потерями групповую скорость нельзя определять как игрА) / еф, уменьшение 5 с ростом частоты не свидетельствует о различии знаков фазовой и групповой скоростей, как это имеет место при аналогичном поведении дисперсионной характеристики в двухслойном волноводе без потерь. При k 0 3 - 0 6 ( рис. 4.3) колеблющаяся энергия уменьшается с частотой быстрее, чем 1 / ко. Это приводит несмотря на рост частоты к уменьшению фазовой постоянной. Уменьшение колеблющейся энергии объясняется резким увеличением потерь в пленке, вызывающем при постоянном потоке мощности перераспределение между колеблющейся энергией, запасенной в волноводе W вне пленки, и энергией потерь. [27]
Можно утверждать, что частоты, на которых Р Р 0, всегда совпадают с критическими частотами соответствующих волн двухслойного волновода без пленки с параметрами, определенными с помощью описанной процедуры. В самом деле, равенство Р 0 говорит о том, что поле не взаимодействует с пленкой. Следовательно, в этом случае волна в волноводах с пленкой и без пленки должна иметь одинаковые характеристики. Действительно поперечные волновые числа на частоте, которую называем критической, в волноводе с пленкой удовлетворяют уравнению (4.7), из которого определяются критические частоты волн HEnm в двухслойном волноводе без пленки. [28]
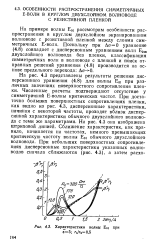 |
Характеристики волны EOI при. 5. п / г20 5. [29] |
На рис. 4.3 представлены результаты решения дисперсионного уравнения (4.8) для волны E0i при различных значениях поверхностного сопротивления пленки. Численные расчеты подтверждают отсутствие у симметричной Е - волны критических частот. При достаточно больших поверхностных сопротивлениях пленки, как видно из рис. 4.3, дисперсионные характеристики, начиная с некоторой частоты, проходят вблизи диспер-синной характеристики обычного двухслойного волновода с теми же параметрами. На рис. 4.3 она изображена штриховой линией. Сближение характеристик, как правило, начинается на частотах, немного превышающих критическую частоту волны E0i обычного двухслойного волновода. [30]
Страницы: 1 2