Периодический волновод

Cтраница 1

Расчет периодического волновода с произвольным числом различных однородных областей в периоде / / Современные проблемы механики сплошной среды: Труды 4 - й междунар. [1]

Полосы пропус-кония периодического волновода, относящиеся к волне с мультипликатором р, имеющей т азимутальных вариаций, при идеально жесткой границе ( краевая задача (5.2) - (5.3)), поверхность которой задается уравнением (5.32), определяются в первом приближении по s следующим образом. [2]

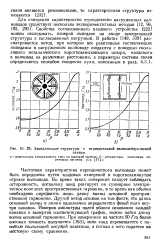Замедляющие структуры с отрицательной взаимоиндуктивной. [3]

Частотная характеристика периодического волновода может быть определена путем зондовых измерений в короткозамкнутом отрезке волновода. Во время таких измерений следует соблюдать, осторожность, поскольку зонд реагирует на суммарное электрическое поле всех пространственных гармоник, в то время как обычно необходимо определить лишь длину волны основной пространственной гармоники. Другой метод основан на том факте, что длина, основной волны в линии однозначно определяется фазой поля внутри канавок. [4]

Если из периодического волновода сделать кольцо, соединив вход с выходом, то также получится резонансная система. В этом случае при резонансе на длине волновода должно укладываться целое число полных волн и, как и ранее, на дисперсионной кривой будет расположена группа дискретных резонансных частот соответствующих видов колебаний. [5]

Полосы пропускания периодических волноводов / / Учен. [6]

Предполагалось, что периодический волновод имеет радиус а 30 мм и образован из проводников круглого поперечного сечения. [7]

К задаче Р %. [8]

Расчет показывает, что путем соответствующего подбора параметров периодического волновода можно управлять его волнопроводящими и резонансными свойствами. [9]

В целом же вся теория возбуждения гладких волноводов переносится без изменений на периодические волноводы ( мы воспользуемся этим обобщением в гл. [10]

Будем рассматривать модель ЛОВ, которая представляет собой согласованный на концах отрезок периодического волновода длины L, пронизываемый электронным пучком с невозмущенной скоростью VQ. [11]

Вышеприведенные формулы позволяют проследить связь между дисперсионными свойствами волн в однородном круговом цилиндре с их свойствами в замедляющих системах с периодически модулированными границей и средой. При к-0 периодический волновод переходит в круговой цилиндр с однородной средой и идеально проводящей границей, при этом по формуле (6.27) получаем при х - 0 хорошо известные значения постоянных распространения для цилиндра. [12]

Заметим, что в частотной области, для которой - 21 к I Д / 3 2Ы, величина 0 имеет мнимую часть. Эта область называется запрещенной зоной периодического волновода, изображенного на рис. 11.6; формально она совпадает с аналогичной зоной периодической слоистой среды ( см. разд. Падающие волны, частоты которых соответствуют этой области, являются затухающими на гофрированном участке и испытывают сильное отражение при условии, что длина взаимодействия L достаточно большая. [13]

Неоднозначность связана с тем, что волновым вектором данной волны можно назвать волновое число любой из пространственных гармоник. В целом же теория возбуждения гладких волноводов переносится без изменений на периодические волноводы, чем мы и воспользуемся при анализе приборов с длительным взаимодействием в последующих лекциях. [14]

В третьей и четвертой главах приведен статистический анализ свойств передачи тракта в зависимости от статистических свойств его нерегулярностей. Изложены основные результаты теории нерегулярных многоволновых волноводов, свойства которых изменяются случайным образом от тракта к тракту. Исследуются статистические параметры флюктуации амплитудной и фазовой характеристик линии при перестройке частоты, при переходе от одного тракта к другому, при изменении длины линии. Статистическим аналогом отмеченного свойства периодических волноводов является следующий результат: из всего спектра нерегулярностей длинной линии в формировании какой-либо паразитной волны участвует только компонента, соответствующая длине волны биений. Выясняются условия устойчивого распространения рабочей волны. Полученные результаты позволяют рассчитывать реальные мнаговолновые волно-водные линии. [15]

Страницы: 1 2