Бегущие волны
Cтраница 1
Бегущие волны Вообще, решения вида бегущей волны у уравнения с частными производными появляются как специальные инвариантные относительно группы решения, когда рассматриваемая группа является группой сдвигов в пространстве независимых переменных. [1]
Бегущие волны распространяются по линии бесконечной протяженности, по длине которых условия распространения не меняются. [2]
Бегущие волны могут существовать при любых значениях механической энергии, так что уровни энергии при S мсх С / 0 расположены непрерывно. [3]
Бегущие волны в реальном волноводе расходуют энергию на нагревание стенок. Этот расход определяется конечной проводимостью материала стенок. Следовательно, электрическое поле в действительности не строго перпендикулярно к стенкам, а вектор Умова-Пойнтинга не строго параллелен оси волновода. [4]
Бегущие волны в газовой / / Лаврентьев. [5]
Бегущие волны fi ( t XIC0) распространяются без искажений, причем любое значениеft const переносится с постоянной скоростью С0, которая и называется скоростью распространения волны. [6]
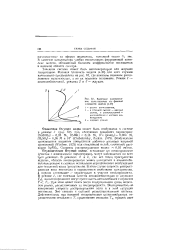 |
Взаимное расположение нуль-изоклин па - фазовой плоскости модели. [7] |
Периодические бегущие волны, исходящие из неолпородности ( участка с измененными параметрами), могут наблюдаться во всех трех режимах. В режимах 2 и 3, где все тоЧ ] н пространства ждущие, область неоднородности может находиться в автоколебательном режиме и служить источником [ lep и одического возбуждения для остальной част пространства - В этом случае скорость распространения волн постоянна п определяется свойствами пространства, а период следования - параметрами в участке неоднородности, В режиме 1, где точечная система автоколебательная ( с периодом Т), на ггеолтторолгюсти могут происходить автоколебания с периодом Ti / V При этом может иметь место синхронизация среды водителем ритма, расположенным на неоднородности. Экспериментально измеряемая скорость распространения волн и в этой ситуации постоянна, Это связано с сильной рела сациошюстыо системм. [8]
Бегущие волны системы квазилинейных уравнений / / Докл. [9]
 |
Бегущие волны. [10] |
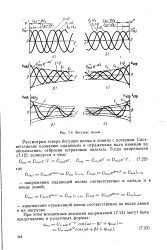
Рассмотрим теперь бегущие волны в линиях с потерями. Соответственно названию падающих и отраженных волн изменим их, обозначения, отбросив штриховые индексы. [11]
Пусть бегущие волны напряжения и тока достигли конца однородной линии, имеющей волновое сопротивление z и замкнутой на сколь угодно сложную цепь с сосредоточенными параметрами. [12]
Рассмотренные здесь бегущие волны складываются друг с другом при встречном распространении падающих и отраженных волн. Характер получающихся при этом волновых процессов изучается в последующих параграфах. [13]
Пусть бегущие волны напряжения и тока достигли конца однородной линии, имеющей волновое сопротивление z и замкнутой на сколь угодно сложную цепь с сосредоточенными параметрами. [14]
Мы получили бегущие волны для тока и напряжения, но в отличие от идеальной линии с t Cj 0 теперь амплитуды тока и напряжения не одинаковы вдоль линии, а экспоненциально уменьшаются при движении волны. Пространственное затухание определяет величина у, растущая с увеличением RI и Сх. Затухание бегущей волны приводит, естественно, к тому, что коэффициент отражения для линии конечной длины никогда не может быть точно равен по модулю единице. Поэтому благодаря потерям в линии не могут образовываться строго стоячие волны; всегда вместе со стоячей волной существует некоторая примесь бегущей волны. [15]
Страницы: 1 2 3 4