Ударные волны - разрежение
Cтраница 1
Ударные волны разрежения были экспериментально обнаружены С. С. Кутателадзе с сотрудниками во фреоне-13. [2]
 |
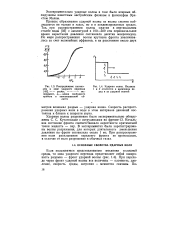
Условия образования ударных волн сжатия и разрежения в среде с аномальной нелинейностью. [3] |
Впрочем, ударные волны разрежения возможны и в обычных ( квадратичных) упругих средах. Это подтверждено ( правда, косвенно, по фазе второй гармоники) в экспериментах Дж. [4]
РО и невозможны ударные волны разрежения Р РО. [5]
При ударной волне разрежения должно происходить убывание энтропии, что невозможно, то есть невозможны ударные волны разрежения. [6]
В зависимости от термодинамических свойств среды в ней могут распространяться не только ударные волны сжатия, но и ударные волны разрежения. [7]
В зависимости от термодинамических свойств среды в ней могут распростраЕ1ЯТься не только ударные волны сжатия, но и ударные волны разрежения. Если же среда обладает аномальными термодинамическими свойствами и ( d2V7dp2) S0, то в такой среде могут распространяться лишь ударные волны разрежения. [8]
При расчете точек, лежащих на фронте ударной волны разряжения, учитывают установленные ранее свойства. Ударные волны разрежения являются волнами слабой интенсивности и их можно рассматривать как упругие. Элементарная волна разрежения за фронтом ударной волны разрежения распространяется медленнее фронта и не изменяет его интенсивности. В рассматриваемой схеме ударные волны разрежения распространяются только сверху вниз. [9]
 |
Схема опыта для определения разрушающих напряжений при отколе. 1 - ВВ. 2 - основная плита. 3 - пластины. [10] |
На рис. 19.52 показана схема волн при соударении железных пластины и плиты. В точке К встречаются две ударные волны разрежения и происходит разрушение плиты. [11]
При возвратном движении рабочего органа создается ряд элементарных волн разрежения, которые не суммируются. Это доказывает, что при колебательном движении рабочего органа в водовоздушной смеси не могут распространяться снизу вверх ударные волны разрежения. Поскольку температуру с обеих сторон фронта ударной волны можно считать одинаковой, то энергия, передаваемая рабочим органом ударной волне, расходуется только на механическую работу - на сжатие смеси и ее движение. [12]
В зависимости от термодинамических свойств среды в ней могут распростраЕ1ЯТься не только ударные волны сжатия, но и ударные волны разрежения. Если же среда обладает аномальными термодинамическими свойствами и ( d2V7dp2) S0, то в такой среде могут распространяться лишь ударные волны разрежения. [13]
Ветвь адиабаты Гюгонио ОА при rii T ] O расположена под адиабатой Пуассона, поэтому для ударных волн разрежения энтропия убывает. Однако такое заключение находится в противоречии со вторым началом термодинамики: dS O. Поэтому ударные волны разрежения, формально содержащиеся в соотношениях Гюгонио, существовать не могут. Такой вывод мы сделали для идеального газа, однако он справедлив и в общем случае при сравнительно слабых ограничениях на вид уравнений состояния и носит название теоремы Цемплена. [14]
Как упомянуто выше, вычислительная схема Роу основана на решении линеаризованной задачи Римана и, следовательно, использует при построении решения только разрывы. Таким образом, волны разрежения в решении задачи Римана заменяются ударными волнами разрежения. Это опасная процедура, так как нефизичные ударные волны разрежения могут появиться и при решении глобальной задачи. Специальные процедуры энтропийной коррекции, разработанные для устранения этого явления, представлены в разд. [15]
Страницы: 1 2