Температурные волны

Cтраница 1

Температурные волны распространяются с определенной скоростью от места возбуждения в субмикроскопических и микроскопических частицах поверхностного слоя в глубь массы тела. [1]

Температурные волны сравнительно быстро затухают по глубине массы тела. [2]

Распространяющиеся высокочастотные температурные волны в поверхностном слое в процессе трения создают высокие знакопеременные градиенты температуры, которые при неравномерном электрическом поле на трущейся поверхности вызовут в поверхностном слое термодиффузионные процессы, а следовательно, этим будут устранены условия для диффузии азота и кислорода в глубинные слои трущейся поверхности. [3]

Более мелкие температурные волны сглаживаются из-за обычной молекулярной теплопроводности. [4]

Опыт показывает, что температурные волны с периодом в одни сутки распространяются внутрь Земли со скоростью 1 м / сут. [5]

От места контакта резания распространяются температурные волны с весьма высокими градиентами, и измерять нестационарный тепловой поток приборами - задача весьма сложная. Что же касается температуры в глубинных слоях ( стационарный поток), то она может и соответствовать указанным величинам, но для анализа протекания рассматриваемого процесса этого недостаточно. [6]

В рассмотренном случае периодического распространения тепла предполагалось, что температурные волны являются простыми гармоническими. [7]

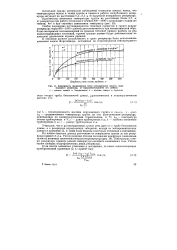Зависимость продвижения зоны охлажденного грунта, окружающего резервуар, от продолжительности его работы. [8]

Детальный анализ материалов наблюдений позволяет сделать вывод, что температурные волны в толще грунта в процессе работы заглубленного резервуара затухают на расстоянии 0 4 - 0 5 м от наружной поверхности резервуара. [9]

Упругие поперечные ( поверхностные) и пластические волны, как и температурные волны, проникают на небольшую глубину и охватывают субмикроскопические частицы материала поверхностного слоя. [10]

Основываясь на результатах точной теории, мы можем с самого начала исключить из рассмотрения изобарические флуктуации энтропии ( температурные волны), дающие очень узкую - 107 гц несмещенную линию в спектре. Тем самым мы отказываемся от рассмотрения медленных релаксационных процессов ( т - 10 - 8 сек), которые могут взаимодействовать с температурными волнами; результат такого взаимодействия можно проанализировать только на основе полной теории. [11]

Сравнивая результат в-ычисления толщины слоя заметного колебания температуры в этом примере с результатом примера 14, усматриваем, что температурные волны с ( конечным коэффициентом теплоотдачи я на поверхности стен имеют несколько меньшую - глубину проникновения, чем волны в примере 14, для которых а со. [12]

Тисса ( 1938) и Л. Д. Ландау ( 1941) предсказали, что в этой системе наряду с обычными звуковыми волнами должны существовать температурные волны, распространяющиеся с некоторой скоростью а2 - Эти волны были названы вторым звуком. По Тисса, при О К скорость второго звука должна обращаться в нуль, а по Ландау, она должна сохранять конечное значение. Результаты измерений скорости второго звука, выполненных В. П. Пешковым и другими исследователями, находятся в качественном согласии с теорией Ландау. [13]

При чистой и весьма чистой обработке поверхности трения ( V9, V10 - 14) со средней высотой микронеровностей Я 2 мк ( III) температурные волны распространяются достаточно глубоко за пределы гребешков микронеровностей. Так как при этом амплитуда колебаний температурных волн больше шага микронеровностей, то создается большое мгновенное поле высоких температур, приводящее к свариванию плоскостей трущихся пар. [14]

Если начальная безразмерная избыточная температура повсеместно равна нулю ( % 0), то при неравномерной распределении г, по безразмерным координатам / р обязательно возникают температурные волны во всех точках пластины, координаты которых имеют конечные значения, поскольку предельное значение безразмерной избыточной температуры также равно нулю. [15]

Страницы: 1 2 3