Рассматриваемые волны

Cтраница 1

Рассматриваемые волны представляют-собой чисто магнитные колебания вектора намагниченности, при которых электрического поля не возникает. Они называются спиновыми волнами и определяют многие магнитные, тепловые и электрические свойства ферромагнетиков. [1]

Поэтому рассматриваемые волны могут существовать даже в случае, когда их частота значительно меньше частоты соударений электронов с частицами газа. [2]

Обе рассматриваемые волны заполняют весь В. Если волны возбуждаются в В. [3]

Заметим, что все рассматриваемые волны подвержены дисперсии. [4]

Действительная часть Ф описывает рассматриваемые волны в случае достаточно малых амплитуд. [5]

Стоячие волны ( сечение водной поверхности вертикальной плоскостью, ортогональной в плане к вертикальной. [6]

Для простоты пояснения примем, что рассматриваемые волны обладают небольшой крутизной. [7]

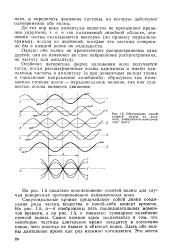Образование одной. стоячей волны из двух, волн, движущихся навстречу / друг другу. [8]

Особенно интересная форма наложения волн получаетсж тогда, когда рассматриваемые волны однотипны и имеют одинаковые частоты и амплитуду ( а при поперечных волнах также и одинаковое направление колебаний): образуется так называемая стоячая волна - парадоксальное явление, так как сущностью волны является движение. [9]

Без ограничения общности мы можем считать m 0; при отрицательном т рассматриваемые волны Кельвина просто меняются местами. Из (8.5.27) ясно, что только 1 / остается ограниченным при больших у, поэтому U должно быть отброшено. [10]

Обе рассматриваемые волны заполняют весь В. Если волны возбуждаются в В. [11]

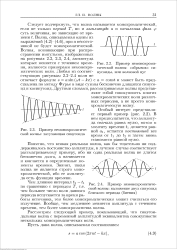Пример ыемонохроматргае-ской волны. затухающая синусоида.| Пример немонохроматиче. [12]

Фурье в виде суммы бесконечно длящихся синусоид и косинусоид. Другими словами, рассматриваемые волны представляют собой совокупность многих монохроматических волн различных периодов, а не просто монохроматическую волну. [13]

Я сохраняет прежнее направление. Обе рассматриваемые волны заполняют весь В. Если волны возбуждаются в В. [14]

Волны, возникающие при распространении импульсов, изображенных на рис. 2.2, 2.3, 2.4, амплитуда которых меняется с течением времени, являются примерами немонохроматических волн. Любая из соответствующих рис. 2.2 - 2.4 волн не отвечает формуле s a sin ( соt - kx) с а const и может быть представлена по методу Фурье в виде суммы бесконечно длящихся синусоид и косинусоид. Другими словами, рассматриваемые волны представляют собой совокупность многих монохроматических волн различных периодов, а не просто монохроматическую волну. [15]

Страницы: 1 2