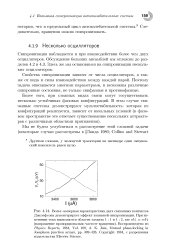
Больший ансамбль
Cтраница 2
Синхронизация наблюдается и при взаимодействии более чем двух осцилляторов. Обсуждение больших ансамблей мы отложим до разделов 4.2 и 4.3. Здесь же мы остановимся на синхронизации нескольких осцилляторов. [17]
Спин и Паули принцип. При рассмотрении больших ансамблей фермионов ограничение на заполнение состояний учитывается статистикой Ферми - Дирака. [18]
Мы скажем, что ансамбль, определенный таким образом, является канонически распределенным, и назовем постоянную в его модулем. Он, очевидно, является в нашем обозначении большим ансамблем. [19]
 |
Образование откольной трещины в двумерной модели, содержащей.| Образование откольной трещины в трехмерной модели, содержащей. [20] |
Исследование кинетики процессов, происходящих в зоне образования откольной трещины, требует рассмотрения чрезвычайно больших ансамблей частиц, что возможно только при использовании многопроцессорных вычислительных систем. [21]
Если система передачи-приема или звукозаписи-звуковоспроизведения является одноканальвой ( монофонической), то даже аппаратура с параметрами, соответствующими высшему lyiaccy, не даст натурального звучания в том смысле, что в звуковоспроизведении не будет акустической перспективы - слушатели будут чувствовать, что звук излучает небольшая поверхность. Отсутствие акустической перспективы особенно заметно при воспроизведении звучания симфонического оркестра, хора и тому подобных больших ансамблей. [22]
Термодинамика как раздел математической физики, в основе которого1 лежат два закона ( первый и второй законы термодинамики), изучает равновесие и направление самопроизвольно протекающих процессов в системах взаимодействующих макроскопических тел. Вследствие того что свойства систем и характер физико-химических процессов в технологии интегральных схем определяются взаимодействием больших ансамблей атомов ( или молекул), термодинамика является одной из основополагающих наук, используемых при исследовании технологических процессов. [23]
Таким образом, термодинамический порог самоорганизации достигается, когда термодинамическая ветвь претерпевает первую бифуркацию. В точке бифуркации динамика системы определяется существующими в системе нелинейностями. Когерентное поведение больших ансамблей атомов или молекул становится возможным и при благоприятных условиях приводит к образованию диссипативных структур. Можно сказать также, что за термодинамическим порогом самоорганизации мы вступаем в область синергетики: огромное число степеней свободы макроскопических систем резко сокращается. Миллиарды и более молекул оказываются подчинены, если воспользоваться терминологией Хакена [1.54], небольшому числу мод. [24]
Возможности статистической трактовки полимеров связаны со следующими обстоятельстнами. Полимерные цепи состоят из большого числа однотипных звеньев, и, как будет показано далее, представляют собой гибкие образования. Статистическое рассмотрение основывается на существовании больших ансамблей объектов, обладающих независимыми степенями свободы. Полимерные цепи дейстпительно являются такими ансамблями. [25]
Первая часть книги описывает синхронизацию без формул, на качественном уровне. Основные эффекты проиллюстрированы экспериментальными примерами и рисунками; представлена история исследований в этой области. Во второй и третьей частях на строгом уровне излагаются как классические результаты по синхронизации периодических автоколебаний, так и последние достижения в исследовании хаотических систем, больших ансамблей и колебательных сред. Монография адресована широкой аудитории - от студентов до квалифицированных исследователей в области физики, прикладной математики, инженерных и естественных наук. [26]
Вследствие дефицита электронов в металлических телах не могут образоваться обычные парно-электронные связи. В таких случаях связь осуществляется за счет коллективного электронно-атомного взаимодействия. Химическая связь в металлах является многоцентровой, ненасыщенной и ненаправленной. Теоретически поведение электронов в металле удовлетворительно описывается сг точки зрения зонной теории, которую качественно можно представить как результат приложения ММО к большим ансамблям частиц порядка постоянной Авогадро - 1023 атомов. [27]
Показывается, что вода является полностью водородосвязанной системой с широким распределением энергий водородной связи и О-О - растоя-ний. Сравнивается термодинамические свойства воды и ртути. Затем анализируются свойства воды, определяемые взаимными поступательными движениями молекул Н % 0 в жидкости, явления переноса. Поступательные движения молекул в жидкости представляют собой наиболее характерное свойство жидкого состояния, определяющее высокий уровень внутренней энергии жидкости по сравнению с кристаллом, и обусловлены взаимодействием больших ансамблей молекул. Анализ данных по различным явлениям переноса в жидкой воде показывает, что средние значения амплитуды атомных колебаний в жидкой воде имеют значение, близкое к - 0 6 А. Большое значение коэффицента трения в воде по сравнению с коэффициентом трения в других жидкостях при температуре плавления показывает, что в воде сильно межмолекулярное взаимодействие, определяемое ближайшими соседями. В этой главе обсуждаются результаты изучения свойств воды методом ЯМР ( ядерного магнитного резонанса) и молекулярного рассеяния света. Рассматриваются свойства воды, обусловленные диссоциацией молекул НгО на ионы. [28]
В зависимости от характера передаваемых программ звук может приниматься одним пли несколькими микрофонами. Выбор числа и типа микрофонов зависит от конкретных условий. Для передачи речи диктора нужен один микрофон. Однако па дикторском пульте устанавливают, как правило, два микрофона, один из которых является резервным. При передаче и записи больших ансамблей число микрофонов может превышать двадцать. Качество звучания передаваемых программ во многом зависит от качества применяемых микрофонов. Поэтому в студийной практике и при трансляции спектак-тей и концертов используют только высококачественные микрофоны. [29]
Принцип неопределенности Гейзенберга вовсе не сводится к утверждению о том, что причинные связи квантовых явлений находятся за пределами возможности их обнаружения; он со всей очевидностью предполагает, что таких связей просто не существует. Именно к такому выводу пришел сам Гейзенберг. С появлением принципа неопределенности классическая причинность и детерминизм утрачивают смысл. Квантовая механика оперирует только статистическими понятиями. Она не дает точного описания отдельной частицы и точного предсказания ее поведения. Однако квантовая механика позволяет с высокой точностью предсказывать поведение больших ансамблей частиц. [30]
Страницы: 1 2 3