Нулевая частота
Cтраница 3
Большое усиление на нулевой частоте постоянного воздействия и малое усиление на частотах устойчивых звеньев позволяют в этом частном случае системы с обратной связью достичь компромисса между инвариантностью и устойчивостью. Заметим, что на нулевой частоте - собственной частоте интегрирующего управляющего устройства - контур имеет бесконечно большое усиление. Поэтому при замыкании системы нулевой полюс перемещается влево вдоль действительной отрицательной полуоси до значения, приближенно равного - kr Переходные процессы в системе и свободные движения в основном определяются этим корнем. Система имеет малое быстродействие. [31]
Большое усиление на нулевой частоте постоянного воздействия и малое усиление на частотах устойчивых звеньев позволяют в этом частном случае системы с обратной связью достичь компромисса между инвариантностью и устойчивостью. Заметим, что на нулевой частоте - собственной частоте интегрирующего управляющего устройства - контур имеет бесконечно большое усиление. Поэтому при замыкании системы нулевой полюс перемещается влево вдоль действительной отрицательной полуоси до значения, приближенно равного - kr Переходные процессы в системе и свободные движения в основном определяются этим корнем. Система имеет малое быстродействие. [32]
Их называют также нулевыми частотами. [33]
Полоса пропускания простирается от нулевой частоты до частоты среза / р, а полоса затухания - ( г / гр Д бесконечности. [34]
Полоса затухания простирается от нулевой частоты до частоты среза / гр, а полоса пропускания - от / гр до бесконечности. [35]
Коэффициент передачи фильтра на нулевой частоте равен 1, на частоте среза - заданному уровню пульсаций в полосе задерживания. При со - оо коэффициент передачи равен нулю при нечетном порядке фильтра и уровню пульсаций - при четном. [36]
Зная сопротивление двухполюсника на нулевой частоте ( постоянный ток) и используя свойство 2, легко определить характер первого резонанса в двухполюснике. Так, если на нулевой частоте Z ( jo)) 0, то в начале координат располагается нуль; он не относится ни к какому резонансу, гак как на постоянном токе резонанса не происходит. За нулем следует полюс, при котором сопротивление двухполюсника обращается в бесконечность, что характерно для резонанса токов. Таким образом, первым наступает резонанс токов. Если же на нулевой частоте Z ( / GO) стремится к бесконечности, то в начале координат располагается полюс, а затем по свойству 2 располагается нуль, что свидетельствует о наличии резонанса напряжений. [37]
Последняя существует только при нулевой частоте и поэтому является не спектральной плотностью, а общим количеством мощности в нулевой полосе частот, обладающей бесконечной спектральной плотностью. [38]
Рассмотрение коэффициента усиления на нулевой частоте проливает новый свет на значение отрицательного гистерезиса. С ростом отрицательного гистерезиса в системе амплитуда колебаний уменьшается, а коэффициент усиления Л / Г0 в соответствии с уравнением (11.31) растет. На границе устойчивых колебаний амплитуда равна ширине петли гистерезиса, а коэффициент усиления на нулевой частоте равен бесконечности. Так как после прохождения коэффициента усиления через бесконечность он изменяет знак, то за этой точкой система останавливается в одном из двух устойчивых положений. [39]
Точка амплитудно-фазовой характеристики на нулевой частоте соответствует статическому режиму работы системы. Часто эта точка бесконечно удалена от начала координат. [40]
За ординату, соответствующую нулевой частоте, примем удвоенное значение - постоянной слагающей ряда Фурье. [41]
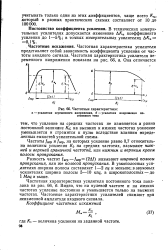 |
Частотные характеристики. [42] |
Видно, что на нулевой частоте и на низких частотах усиление постоянно и уменьшается только на высоких частотах. [43]
Зная сопротивление двухполюсника на нулевой частоте ( постоянный ток) и используя свойство 2, легко определить характер первого резонанса в двухполюснике. Так, если на нулевой частоте Z ( yro) 0, то в начале координат располагается нуль; он не относится ни к какому резонансу, так как на постоянном токе резонанса не происходит. За нулем следует полюс, при котором сопротивление двухполюсника обращается в бесконечность, что характерно для резонанса токов. Таким образом, первым наступает резонанс токов. Если же на нулевой частоте Z ( yro) стремится к бесконечности, то в начале координат располагается полюс, а затем по свойству 2 располагается нуль, что свидетельствует о наличии резонанса напряжений. [44]
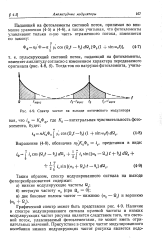 |
Спектр частот на выходе оптического модулятора. [45] |
Страницы: 1 2 3 4