Вращательное квантовое число

Cтраница 2

Зависимость внутренней энергии двухатомной молекулы от расстояния между ядрами. [16]

Планка; п, - вращательное квантовое число. [17]

В этом уравнении г - вращательное квантовое число, определяющее высоту вращательного уровня, / - момент инерции по отношению к двум взаимно перпендикулярным осям, проходящим через центр тяжести молекулы перпендикулярно ее оси. [18]

Зависимость внутренней энергии двухатомной молекулы от расстояния между ядрами. [19]

Планка; п, - вращательное квантовое число. [20]

Для не слитком больших значений вращательного квантового числа в выражениях для ЗЛ ( И к), ( n - K 2 обычно бывает достаточно оставлять только члены со степенями у не выше первой. [21]

Поэтому возможны переходы с изменением вращательного квантового числа на единицу. [22]

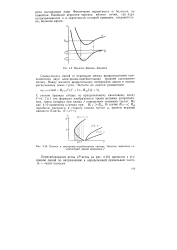Принцип Франка - Кондона.| Полосы в электронно-колебательном спектре. Частоты переходов соответствуют целым значениям. [23]

С учетом правила отбора по вращательному квантовому числу / /, / 1 эта формула изображается тремя ветвями ( параболами), точки которых при целых J определяют значения частот. В случае Bn v Bnv параболы раскрыты в сторону низких частот со, причем верхней является У. [24]

Квантовые числа Л и б1 и вращательное квантовое число могут комбинировать между собой различным образом ( различные комбинации называются случаями Гунда а, Ъ, с, d), приводя к появлению целого ряда энергетических уровней. [25]

Здесь мы отмстим только, что вращательное квантовое Число / изменяется обычно на несколько единиц, причем среднеквадратичная переданная энергия ( ДЕ) 2ир пропорциональна квадрату фурье-компоненты частоты со; от анизотропной части потенциала взаимодействия. Именно последнее выражает проявление адиабатического принципа: чем меньше скорость изменения возмущающего действия на систему ( и рассматриваемом случае - ротатор), тем меньше вероятность изменения ее состояния. [26]

Кроме приведенных нами правил отбора для вращательных квантовых чисел, имеются также правила отбора, касающиеся свойств симметрии вращательных уровней. [27]

Как видно, эта разность пропорциональна вращательному квантовому числу J и обратно пропорциональна моменту инерции J0 молекулы. Формула (15.10) дает ряд равностоящих друг от друга спектральных линий чистого вращательного спектра, расположенных в далекой инфракрасной области с длиной волны порядка сотен микрон. [28]

Как видно, эта разность пропорциональна вращательному квантовому числу J и обратно пропорциональна моменту инерции J0 молекулы. Формула (15.10) дает ряд равноотстоящих друг от друга спектральных линий чистого вращательного спектра, расположенных в далекой инфракрасной области с длиной волны порядка сотен микрон. [29]

Здесь, как обычно, f обозначает вращательное квантовое число для верхнего состояния J J-для нижнего состояния. [30]

Страницы: 1 2 3 4