Вывод - уравнение - теплопроводность
Cтраница 1
Вывод уравнения теплопроводности в данном контексте сам по себе не представляет особого интереса. [1]
Для вывода уравнения теплопроводности выделим внутри тела О некоторый объем D, ограниченный гладкой поверхностью 5, и рассмотрим изменение количества тепла в это. [2]
При выводе уравнения теплопроводности ( 83) мы предполагали, что в рассматриваемом теле отсутствуют источники тепла. [3]
В-третьих, вывод уравнения теплопроводности, который мы выполняем для элемента конечных размеров - hxhyhz, по той же схеме можно выполнить и для бесконечно малого элемента dxdydz. [4]
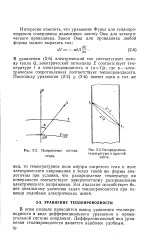 |
Направление потока.| Распределение температуры в простой плите. [5] |
В этом разделе приводится вывод уравнения теплопроводности в виде дифференциального уравнения в прямоугольной системе координат. [6]
Какие гипотезы используются при выводе уравнения теплопроводности. [7]
Если вспомнить приводившийся в § 3 вывод уравнения теплопроводности, то легко заметить, что он как раз состоял в получении закона сохранения тепла для бесконечно малого параллелепипеда. Интегральным тождеством, которое было выписано, нам будет удобно в некоторый момент воспользоваться. [8]
Здесь же в рамках термодинамики линейных необратимых процессов дается вывод уравнения теплопроводности с членом, зависящим от деформации. Эти уравнения вместе с уравнениями движения, соотношениями между деформациями и перемещениями, известными из классической теории упругости, а также начальными и граничными условиями образуют замкнутую систему уравнений, описывающую задачу термоупругости, в которой поля деформации и температуры связаны между собой. Постановка задачи термоупругости рассматривается в § 1.7. В зависимости от характера механических и тепловых воздействий и условий теплообмена в постановку задачи термоупругости вносятся упрощающие предположения. [9]
Далее ( § 1.5) излагается термодинамический подход к выводу соотношений между напряжениями и деформациями, содержащих температурные члены. С другой стороны, в рамках термодинамики линейных необратимых процессов дается вывод уравнения теплопроводности с членом, зависящим от деформации. Полученная система уравнений описывает так называемую связанную задачу термоупругости, в которой температурное поле и поле деформаций рассматриваются связанными между собой. [10]
Зависимость пространственного распределения температуры от времени выражается дифференциальным уравнением теплопроводности. Задача нахождения распределения температуры сводится к решению этого уравнения. Вывод диференци-ального уравнения теплопроводности базируется на законе Фурье ( III, 3) и законе сохранения энергии, который в данном случае выражается в том, что разность количеств тепла, вошедшего за время dt в некоторый элементарный объем, вырезанный в теле, и вышедшего из него вследствие теплопроводности, полностью расходуется на изменение температуры рассматриваемого элементарного объема. [11]
Страницы: 1