Результирующее движение

Cтраница 2

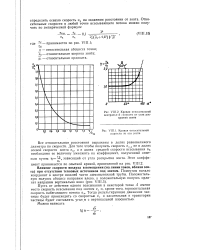Кривая относительной центральной скорости от угла раскрытия зонта.| Кривая относительной скорости по оси зонта. [16]

Тогда результирующее движение частицы будет происходить со скоростью и, и касательная к траектории частицы будет составлять угол а с вертикальной плоскостью. [17]

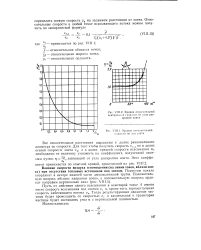Кривая относительной центральной скорости от угла раскрытия зонта.| Кривая относительной скорости по оси зонта. [18]

Тогда результирующее движение частицы будет происходить со скоростью vr и касательная к траектории частицы будет составлять угол а с вертикальной плоскостью. [19]

Вид результирующего движения зависит от амплитуд составляющих колебаний, от отношения между их частотами и от их фазового сдвига. [20]

Движение электрона в магнитном поле. [21]

Траекторая результирующего движения имеет вид винтовой линии, радиус и шаг которой зависят от модуля и направления векторов скорости электрона и магнитного поля. [22]

Следовательно, результирующее движение должно происходить по спирали с уменьшающимся радиусом и в конечном счете электроны должны упасть на положительно заряженное ядро. [23]

Итак, результирующее движение, обусловленное парой угловых скоростей будет состоянием мгновенных поступательных скоростей. [24]

Итак, результирующее движение имеет энергию, равную сумме энергий составляющих колебаний, и никак не зависит от разности фаз между ними. [25]

Следовательно, результирующее движение представляет собой вращение около мгновенной оси. С какой угловой скоростью происходит это вращение. [26]

Является ли результирующее движение системы с двумя степенями свободы гармоническим колебанием. [27]

Найдем характер результирующего движения тела, считая, что ось вращения перпендикулярна поступательной скорости. [28]

При винтовой заточке результирующее движение по существу не является винтовым, так как суммарное поступательное перемещение не параллельно оси вращения. Поэтому задняя поверхность сверла в общем случае может быть невинтовой. [29]

Таким образом, результирующее движение также является вращением твердого тела вокруг неподвижной точки. Поэтому все сказанное в предыдущем параграфе относительно определения скоростей и ускорений точек твердого тела, нахождения уравнений подвижного и неподвижного аксоидов, углового ускорения может быть применено в данном случае. [30]

Страницы: 1 2 3 4