Аргумент - синус
Cтраница 3
 |
Встроенный волоконный интерферометр Фабри-Перо. [31] |
В том случае, если ВВИФП работает на пропускание, его рабочая характеристика может быть описана выражением (4.77), в котором аргумент синуса должен быть заменен выражением 2тт /, где 8 - расстояние между торцами световодов. [32]
Поэтому в той области значений т, где с уровнем j / ( t) приходится считаться, сомножитель 1 - т / Гс в аргументе синуса практически равен единице. [33]
Действительно, фаза - линейная комбинация времени ( в выражении ( 8) w0 постоянно для данной системы, q0 - фиксировано) и, являясь аргументом синуса, представляет собой угловую величину. [34]
При k 6c 1, чему соответствуют верхние знаки в аргументе синусов, образуется система величин ( токов) прямой последовательности; при k - 6с - 1 ( нижние знаки в аргументах синусов) сисгема величин ( токов) обратной последовательности. [35]
При k & c 1, чему соответствуют верхние знаки в аргументе синусов, образуется система величин ( токов) прямой последовательности; при k - 6с - 1 ( нижние знаки в аргументах синусов) система величин ( токов) обратной последовательности. [36]
Аргумент синуса в формулах (1.9) и ( 1.9), представляющий фазу колебаний величины s в произвольной точке М, обозначается через Ф8 и называется фазой волны в этой точке. Из ( 1.9) следует, что колебания в произвольной точке М оси ОХ отстают по фазе от колебаний в точке О на кх. [37]
Аргумент синуса в формулах (1.9) и ( 1.9), представляющий фазу колебаний величины s в произвольной точке М, обозначается через Ф8 и называется фазой волны в этой точке. ОХ отстают по фазе от колебаний в точке О на кх. [38]
Аргумент синуса в формулах (1.9) и ( 1.9), представляющий фазу колебания величины s в произвольной точке М, обозначается через Фх и называется фазой волны в этой точке. Из ( 1.9) следует, что колебания в произвольной точке М оси ОХ отстают по фазе от колебаний в точке О на кх. [39]
Итак, нам известно, что функция, выражающая зависимость амплитуды скоростей или деформаций от величины к ( расстояния от левого конца стержня), может быть либо синусом, либо косинусом. Так как аргументом синуса или косинуса должна быть величина безразмерная, а независимая переменная х имеет размерность длины, то в аргумент синуса или косинуса должно входить отношение х к некоему параметру, имеющему размерность длины; конечно, при этом отношении может стоять какой-либо безразмерный множитель. [40]
Амплитуда колебаний изменяется от точки к точке по закону синуса. В точках, для которых аргумент синуса обращается в нуль, амплитуда колебаний падает до нуля. Эти точки все время остаются в покое. Это - уже знакомые нам узловые точки. Следующие узловые точки лежат на расстоянии xl друг от друга. [41]
Амплитуда колебаний изменяется от точки к точке по закону синуса. В точках, для которых аргумент синуса обращается в нуль, амплитуда колебаний падает до нуля. Эти точки все время остаются в покое. Это - уже знакомые нам узлы смещений. Следующие узлы смещений лежат на расстоянии xt друг от друга. [42]
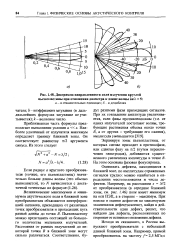 |
Диаграмма направленности поля излучения круглой. [43] |
Наиболее удаленный от излучателя максимум определяет границу ближней зоны. Он соответствует равенству л / 2 аргумента синуса. [44]
Оператор IF в строке 57 предназначен для проверки очередного бита. Первый раз процедура используется для вычисления аргументов синусов и косинусов, а во второй - для окончательного упорядочения данных. [45]
Страницы: 1 2 3 4