Нулевой аргумент

Cтраница 1

Нулевой аргумент подавляет выполнение команды BREAK и внешние прерывания с терминала. Если аргумент равен 1, то команды BREAK и прерывания с терминала разрешены. [1]

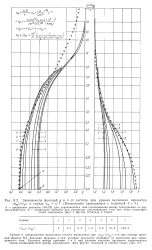Зависимости функций g и h от частоты при разных значениях параметра. [2]

Значение функции g при нулевом аргументе совпадает со значением для лоренцевского газа. [3]

Поскольку функция синуса имеет нулевое значение при нулевом аргументе, можно ожидать, что г з является функцией синуса. [4]

Функция несближения R ( Л) равна 1 при нулевом аргументе, знакопеременна ( как правило) при А / 0 и стремится к нулю при Л 1 - оо. [5]

Заметим, что особые ребра не могут выходить из вершин, соответствующих нулевым аргументам команд остановки. [6]

Функция R ( А) из (2.3.3.18), которую применительно к данному потоку можно назвать функцией несближения, при нулевом аргументе обращается в единицу. [7]

В лемме 2 устанавливается существование линейных операторов, которые вкладывают область определения частичной функции в булев куб меньшей размерности так, что множество образов нулевых аргументов и множество образов единичных аргументов частичной функции имеют незначительное пересечение. Далее показано, что повторное применение леммы 3 сводит вычисление частичной функции / к вычислению последовательности полностью определенных булевых функций, зависящих от последовательно уменьшающегося числа переменных. [8]

Функция RND употребляется только с аргументом. При нулевом аргументе генератор случайных чисел восстанавливается и выдает всегда одно и то же начальное число, с которого начинается генерация псевдослучайной последовательности. [9]

Программу Р, вычисляющую функцию /, для которой справедливо равенство Т ( Р) T ( f), назовем минимальной программой. Нетрудно видеть [7], что в минимальной программе разные команды остановки имеют разные нулевые аргументы. [10]

Число особых ребер обозначим через N. Из каждой вершины, соответствующей вычислительной команде, выходит не более одного особого ребра. Очевидно, что из вершин, соответствующих командам остановки и их нулевым аргументам, особые ребра не выходят. С другой стороны, в каждую вершину, соответствующую команде остановки, входит не более одного особого ребра. [11]

Результат вычисления функции TINY. [12]

Встроенная элементная функция EXPONENT ( х) возвращает экспоненциальную часть аргумента в используемой модели вещественной арифметики. Аргумент должен быть вещественного типа. Результат имеет целый тип. Если аргумент ненулевой, значение результата является экспоненциальной частью аргумента. Порядок должен находиться в пределах диапазона для стандартного целого типа, в противном случае результат неопределенный. Результатом для нулевого аргумента является нулевое значение. [13]

Страницы: 1