Вышеприведенный аргумент

Cтраница 1

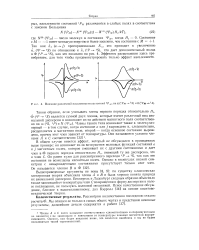Влияние различной населенности состояний 1Р на ф ( 1Рм - - 1S и 0 ( Рм - г5. [1]

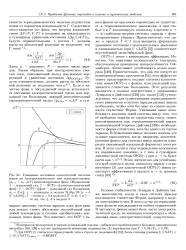
Вышеприведенные аргументы не новы [ 8, 9J: по существу классическая электронная теория объяснила члены Л и Б и была хорошо понята природа их аномальной дисперсии. Беккерель и Ладенбург сходным образом объяснили также зависящий от температуры член С во вращении и форму дисперсии в полосе поглощения, не пользуясь волновой механикой. Ясное качественное обсуждение, близкое к вышеизложенному, дал Кэрролл [34] на основе квантово-механической теории. [2]

Вышеприведенный аргумент выглядит менее убедительным, если вспомнить о случаях, когда правительство оказывалось способным проводить решительную и внушающую доверие антиинфляционную политику в режиме гибких обменных курсов. В подобных случаях сокращение денежной массы приводит к быстрому удорожанию национальной валюты с существенными антиинфляционными последствиями. [3]

Все вышеприведенные аргументы предполагают неизменяемость конфигурации в ходе химической реакции; например, если соединение I превращается в соединение II, то присоединяющаяся группа становится на место замещаемого ею иона. [4]

Многие считают вышеприведенные аргументы очевидными и достаточными. [5]

В соответствии с вышеприведенными аргументами следует ожидать, что 50 - и - поверхности бирадикалоидов будут иметь минимум с рыхлой геометрией, a St - с тесной геометрией. Такое преобладание нельзя объяснить просто указанием на необходимость инверсии спина при суммарной реакции, в силу чего возникает лромежуточный продукт. [6]

Совершенно ясно, что вышеприведенные аргументы применимы для сверхпроводника любой толщины при одном условии, что напряженность поля падает до нуля в некоторой точке внутри него. Следовательно, сверхпроводящая пластина конечной толщины, в которой поле, определяемое уравнением (9.3.14), экранировано, является стабильной. [7]

Таким образом, из всех вышеприведенных аргументов за и против промежуточного образования перекиси водорода при фотосинтезе остается в силе наблюдение Гаффрона о продолжении фотосинтеза у некоторых штаммов Scenedesmus, у которых активность каталазы полностью подавлялась цианидом. Этот опыт подтверждает, что разложение перекиси водорода каталазой не является частью химического механизма фотосинтеза. Гаффрон [37] считает, что перекись водорода не находится среди промежуточных продуктов окисления водорода у адаптированных водорослей. [8]

Это уравнение просто определяет К, но смысл вышеприведенного аргумента состоит в том, что К. [9]

Поскольку для квазиадиабатической области нет никакой достоверной теории, то вышеприведенные аргументы были использованы для предсказания качественных изменений эффективного сечения в зависимости от отношения энергий. Например, с увеличением е эффективное сечение ионизации должно возрастать до довольно пологого максимума порядка величины газокинетического эффективного сечения при е 62 кэв, когда скорость относительного движения становится сравнимой со скоростью электронов атома, участвующих в переходе. Затем сечение должно уменьшаться, вообще говоря, по некоторому степенному закону в зависимости от скорости. [10]

Но даже если мы принимаем закон причинности в качестве всеобщей истины, вышеприведенный аргумент не является решающим. Мы можем предположить, что каждое событие имеет причину и ничто не происходит случайно, все же цепь причин, порождающих будущее событие, хотя и бесконечна, но не достигает настоящего момента. Это может быть объяснено с помощью математической аналогии. [11]

Это пример модуса Вагосо, поскольку он получается в результате подстановки в него. Однако вышеприведенный аргумент не может быть применен к этому силлогизму. Мы не можем допустить, что посылки истинны, потому что предложения Все живые существа суть птицы и Некоторые совы не суть птицы определенно ложны. [12]

Уравнение состояния классической системы ионов на электростатическом или идеально-газовом ( р ( - П ( / гТ компенсирующем фоне. Обозначения. 1 - идеальный газ. 2 - ОСР ( - электростатический фон. 3 - ОСР ( - фон - идеальный газ Больцмана, ne Zn 4 - спинодаль в модели 2 ( др / дУ т О ( Г 3 08. 5 - точка р О в модели 2 ( Г 4. 6 и 7 - то же, что 4 ч 5 в модели 3. [13]

Примечательно, что, как это следует из вышеприведенных аргументов [51], этот эффект не может предотвратить коллапс системы классических ионов ОСР ( -) с фоном, если последний подчиняется статистике Больцмана. Этот результат находится в полном соответствии с доказанным Ленардом и Дайсоном [130] ( см. также [131]) утверждением, что для существования термодинамического равновесия в системе зарядов разных знаков необходимо, чтобы хотя бы один из сортов подчинялся статистике Ферми. Указанная выше неизбежность коллапса такой системы ввиду того, что ее свободная энергия не ограничена снизу, может рассматриваться как термодинамический аналог вышеназванной теоремы Дайсона [130] о необходимости ферми-статистики хотя бы одного из сортов зарядов. В безассоциативных моделях плазмы это условие выполняется, когда, например, компенсирующим фоном для системы ионов является однородно сжимаемый идеальный ферми-газ электронов. [14]

Проведенные рассуждения демонстрируют общность квантового эффекта Холла для систем, в которых поток Ф изменяется адиабатически, оставляя их в основном состоянии ( при Т 0) или в равновесном состоянии - при низких температурах. С другой стороны, обычная проводящая система имеет континуум проводящих состояний при EF, которые чувствительны к потоку, поэтому при конечном V - ( 1 / с) Ф в ней всегда будет иметься некоторая диссипация и вышеприведенные аргументы не будут работать. Это дает еще один способ увидеть важность существования локализованных состояний при EF для проявления КЭХ. [15]

Страницы: 1 2