Модулярная арифметика

Cтраница 1

Модулярная арифметика с внешней редукцией может быть реализована с помощью модулярной арифметики с внутренней редукцией. [1]

Нейронный алгоритм модулярной арифметики, основывающийся на методе понижения разрядности числа, при использовании в качестве модуля чисел Ферма довольно сложен, поскольку требует процедуры определения отношения между количеством разрядов полученного результата и модуля. Последнее не позволяет использовать структуру БПФ при выполнении теоретико-числовых преобразований. Поэтому для эффективного применения теории чисел в нейронных сетях необходимо построить нейросетевой алгоритм конечного кольца по модулю чисел Ферма. [2]

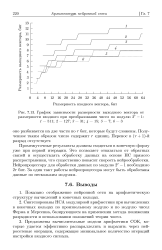График зависимости размерности выходного вектора от. [3]

Синтезированы ПСА модулярной арифметики при вычислениях в конечных кольцах по произвольному модулю и по модулю чисел Ферма и Мерсенна, базирующиеся на применении метода понижения разрядности и использовании положений теории чисел. [4]

Опубликованная литература, посвященная модулярной арифметике, ориентирована главным образом на конструкцию компьютера, так как свойства свободного переноса модулярной арифметики делают ее привлекательной с точки зрения больших скоростей проведения операций. Эта идея была впервые высказана А. Валахом в чехословацком журнале Stroje па Zpracovdni Informaci [ 3 ( 1955), 247 - 295 ], а затем независимо X. Использовать модули вида 2е / - 1 было предложено А. Френкелем [ JACM, 8 ( 1961), 87 - 96 ], а некоторые преимущества модулей такого вида были продемонстрированы А. [5]

В результате разработан нейросетевой алгоритм модулярной арифметики по модулю чисел Ферма и Мерсенна, в котором используемые нейроны - обычные ЛПЭ. В отличие от НС А модулярной арифметики, основывающегося на методе понижения разрядности числа, разработанная простая итерационная структура НСА при использовании в качестве модуля чисел Ферма позволяет применять структуру БПФ в ТЧП. По указанным причинам наиболее эффективно реализовывать ТЧП, обладающие рядом преимуществ перед обычным БПФ, современными нейрокомпьютерными средствами. Числа Ферма и Мерсенна в силу взаимной простоты могут быть использованы в качестве модулей системы остаточных классов для ускоренной нейрообработки. [6]

Таким образом, получен нейросетевой алгоритм реализации модулярной арифметики по произвольному модулю, в котором нет необходимости применения сумматоров по модулю. При использовании в качестве модуля чисел Мерсенна ПСА модулярной арифметики значительно упрощается. [7]

Этот ряд целых чисел недостаточно велик, чтобы модулярная арифметика давала большую скорость, чем обычный метод, и, как правило, использование модулярной арифметики при условии ( 15) выгодно только тогда, когда ту - превышают размер слова. [8]

Вследствие указанных причин возникает принципиальная возможность использования преимуществ модулярной арифметики современными нейрокомпьютерными В Ср. Для этого необходимо представить алгоритм решения указанной задачи в НСЛБ. [9]

Модулярная арифметика с внешней редукцией может быть реализована с помощью модулярной арифметики с внутренней редукцией. [10]

Если же р 2k - 1, то внешняя редукция модулярной арифметики может быть найдена как единственная, соответствующая операции внутренней редукции. [11]

В машинах, в которых допускается одновременное выполнение многих операций, модулярная арифметика может дать значительное преимущество даже для сложения и вычитания: действия относительно различных модулей можно выполнять все одновременно, и тем самым мы получаем существенную экономию во времени выполнения. [12]

Таким образом, разработана двухслойная однородная структура нейронной сети, реализующая модулярную арифметику системы остаточных классов. [13]

Арифметика целых чисел по модулю m может рассматриваться как арифметика остатков или модулярная арифметика. Полная система остатков по модулю m состоит из m целых чисел, по одному представителю из каждого класса эквивалентности. [14]

Таким образом, в целях ускорения нейрообработки и повышения надежности вычислений на основе нейронных сетей разработаны алгоритмы модулярной арифметики. [15]

Страницы: 1 2 3