Комбинация - уравнение
Cтраница 3
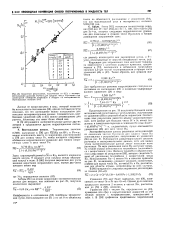 |
Сравнение результатов, полученных из ( 65, с экспериментальными данными ( точки для средних чисел Нуссельта при ламинарной свободной конвекции в воздухе на изотермических вертикальных конусах. [31] |
Данные не представлялись в виде, который позволил бы использовать соотношение ( 58), однако тестовые расчеты показали, что это соотношение можно использовать для описания экспериментальных данных. Следовательно, комбинацию уравнений ( 58) и ( 61) можно рекомендовать для расчета, поскольку она имеет более общий вид. [32]
 |
Положительные направления Л, Q и М. [33] |
Сопоставляя уравнения (7.16), (7.22), (7.23) и (7.26), получим дифференциальные уравнения и граничные условия, описывающие растяжение балки. С другой стороны, комбинация уравнений (7.17), (7.24), (7.25) и (7.27) приводит к дифференциальному уравнению и граничным условиям, определяющим изгиб балки. [34]
Поэтому та одна точка, которая необходима, чтобы использовать комбинацию уравнений (5.10), (3.45) и (3.46) для оценки характера изменений удерживания компонента, может и не быть получена в одном прямом эксперименте. Пс этой причине нам следует полагаться на опыты по градиентному элюирова-нию, которые обеспечат нас необходимой информацией. [35]
Однако при этом рассматривают также разнообразные идеальные тела ( материалы) и точные их законы деформации, которые служат основой для анализа поведения реальных материалов под действием напряжений и разработки экспериментальных методов. Более сложная реакция тел на напряжение определяется сочетанием простейших свойств и описывается реологическими уравнениями, представляющими собой комбинации уравнений, которые характеризуют эти простейшие свойства. [36]
Когда яд подается на слой катализатора непрерывно или импульсами вместе с исходной смесью, он обычно накапливается в начале слоя. Наблюдаемое в результате распределение яда по длине-слоя сильно усложняет интерпретацию данных, и полученные значения относительной активности и концентрации яда являются усредненными для всего слоя. В работе [13] приведены графики зависимости относительной активности от концентрации яда для нескольких комбинаций гипотетических уравнений распределения яда по слою и графики зависимости относительной активности от концентрации яда в элементарном объеме слоя. Оказалось, что относительная активность линейно уменьшается при увеличении концентрации яда во всех случаях, когда имеется конечная концентрация яда на выходе из слоя, т.е. когда существует проскока яда. Наклон прямой зависит от формы уравнений отравления и распределения и от величин параметров этих уравнений. [37]
Матричная алгебра является системой математической стенографии, которая может быть применена для записи системы уравнений в очень компактной форме и для выполнения определенным образом действий над ними. Матрица представляет собой упорядоченную таблицу коэффициентов, расположенных по строкам и столбцам. Когда матрицы применяются к цепям, они могут описывать физическую конфигурацию цепи посредством расположения и типа коэффициентов матрицы. Матрица это не определитель, так как она представляет собой просто таблицу коэффициентов последовательно написанных уравнений и не является комбинацией уравнений, как определитель. Матрица не имеет величины и не может быть вычислена с помощью методов, применяемых для определителей. В матрице число строк и столбцов необязательно будет одинаковым. Матрица системы линейных уравнений образуется с помощью таблицы коэффициентов системы. [38]
Напомним принцип относительности Галилея, который гласит, что физические законы Ньютона и Галилея останутся совершенно неизменными, если от покоящейся системы отсчета мы перейдем в другую, движущуюся равномерно и прямолинейно. Из этого принципа следует, что, просто наблюдая динамическое поведение объектов вокруг нас, мы не можем установить, находимся ли мы в состоянии покоя или движемся равномерно и прямолинейно в каком-то направлении. Предположим теперь, что к законам Ньютона и Галилея мы присоединили уравнения Максвелла. Напомним, что электромагнитные волны Максвелла распространяются с фиксированной скоростью с - скоростью света. Видно, что и тот, и другой результат отличны от фиксированного значения с скорости света в теории Максвелла. И здравый смысл не подвел бы нас: комбинация уравнений Ньютона и Максвелла не удовлетворяет принципу относительности Галилея. [39]
Страницы: 1 2 3