Угловая аберрация
Cтраница 2
Отсюда следует, что коэффициенты аберраций третьего порядка частей системы относятся, как 1: М3, поскольку сумма степеней полевых и зрачковых координат в каждом члене угловой аберрации третьего порядка равна трем. [16]
Если достигнута фокусировка первого порядка по направлениям, коэффициент BI равен нулю; В2 - коэффициент для разброса по скоростям; Вц, Bi2 и Bzz - коэффициенты соответственно для угловой аберрации второго порядка, для смешанной скоростной и угловой аберрации и для чисто скоростной аберрации. [17]
Если достигнута фокусировка первого порядка по направлениям, коэффициент BI равен нулю; В2 - коэффициент для разброса по скоростям; Вц, Bi2 и Bzz - коэффициенты соответственно для угловой аберрации второго порядка, для смешанной скоростной и угловой аберрации и для чисто скоростной аберрации. [18]
Для того чтобы и в пятом порядке получить связь между волновыми аберрациями, необходимо задаться их определенной формой. Дифференцируя это выражение и подставляя полученные угловые аберрации в уравнения (2.8), найдем вполне конкретные выражения для угловых аберраций на сфере G, которые можно проинтегрировать как в третьем, так и в пятом порядке. D &, определим связь между каноническими коэффициентами на двух сферических поверхностях. Промежуточные выкладки довольно трудоемки и громоздки, поэтому приведем лишь конечные результаты. [19]
В первом случае ЭО аберрационных точек отражателя пересекают оптическую ось, во втором - не пересекают. Для малых расстоянии от прибора знак угловой аберрации имеет значение, ибо он определяет характер свечения точек отражателя. Действительно, при отрицательном знаке аберрации точки видны светлыми с того участка оптической оси, на котором ЭО пересекают ее. При положительном знаке аберрации точки не будут видны светлыми при перемещении по оптической оси для любого расстояния от прибора вплоть до бесконечно большого. Таким образом, значение осевой силы света прибора для конечных расстояний зависит от знака аберрации. Для практически бесконечных расстояний ( когда угловой размер отражателя исчезающе мал) знак аберрации не имеет значения, так как две точки с одинаковой аберрацией разных знаков будут светлыми на равных угловых расстояниях от оптической оси. Правда, при Даа светит точка той меридиональной полуплоскости, которая содержит направление наблюдения, а при - Даа светит точка, лежащая в противоположной полуплоскости. [20]
 |
Траектория иона в средней плоскости. [21] |
Для случая симметричного расположения ( I m I m) угловая аберрация второго порядка оказывается равной нулю, еслр. [22]
Для того чтобы и в пятом порядке получить связь между волновыми аберрациями, необходимо задаться их определенной формой. Дифференцируя это выражение и подставляя полученные угловые аберрации в уравнения (2.8), найдем вполне конкретные выражения для угловых аберраций на сфере G, которые можно проинтегрировать как в третьем, так и в пятом порядке. D &, определим связь между каноническими коэффициентами на двух сферических поверхностях. Промежуточные выкладки довольно трудоемки и громоздки, поэтому приведем лишь конечные результаты. [23]
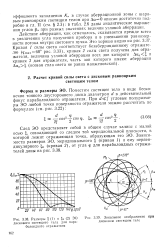 |
Размеры % ( 1 и ( 2 ЭО [ IMAGE ] Зональное отображение при дискового светящего тела для пара - дисковом светящем теле. [24] |
К в случае аберрационной зоны с шаровым равноярким светящим телом при Да 0 описан достаточно подробно в гл. II ( см. § 2.3): в табл. 2.6 даны аналитические выражения углов PC, при разных значениях величин угловой аберрации. [25]
Считаем, как и раньше, что аберрации / - го элемента заданы в плоскости его выходного зрачка, и преобразуем их в плоскость выходного зрачка j 1-го элемента. Однако и в данном случае нельзя ограничиться рассмотрением только волновых аберраций, поскольку в (2.5) входят их производные - угловые аберрации. В связи с этим возникает вопрос об изменении угловых аберраций при переходе через поверхность, разделяющую среды с различными показателями преломления. Волновые аберрации падающего фронта без изменений входят в волновые аберрации фронта, сформированного оптическим элементом ( необходимо, конечно, добавить искажения, вносимые самим элементом), но это не так для угловых величин F. Поскольку волновые аберрации при переходе через поверхность не меняются ( без учета искажений, вносимых элементом), то угловые должны измениться в п / п раз, где п и п - показатели преломления среды до и после поверхности. [26]
Считаем, как и раньше, что аберрации / - го элемента заданы в плоскости его выходного зрачка, и преобразуем их в плоскость выходного зрачка j 1-го элемента. Однако и в данном случае нельзя ограничиться рассмотрением только волновых аберраций, поскольку в (2.5) входят их производные - угловые аберрации. В связи с этим возникает вопрос об изменении угловых аберраций при переходе через поверхность, разделяющую среды с различными показателями преломления. Волновые аберрации падающего фронта без изменений входят в волновые аберрации фронта, сформированного оптическим элементом ( необходимо, конечно, добавить искажения, вносимые самим элементом), но это не так для угловых величин F. Поскольку волновые аберрации при переходе через поверхность не меняются ( без учета искажений, вносимых элементом), то угловые должны измениться в п / п раз, где п и п - показатели преломления среды до и после поверхности. [27]
Первый масс-спектрограф Маттауха-Герцога, описанный впервые Маттаухом ( 1936 и позднее усовершенствованный Эвальдом ( 1946), а также Бьери и др. ( 1955), без изменения основных размеров. Однако затем было установлено, что для одной точки фотографической пластины угловые аберрации второго порядка равны нулю. [28]
Страницы: 1 2