Оптимальное значение - целевая функция
Cтраница 3
В настоящем разделе будет рассмотрен метод суммирования потерь ( отклонений от оптимальных значений целевой функции управления и показателей качества), обусловленных недостоверностью измерительной информации, получаемой от всех измерительных устройств в предположении их исправной работы. Ограничивая потери, мы можем определить величину Ад для каждого измерительного устройства и сформулировать требования к характеристикам точности этих устройств. [31]
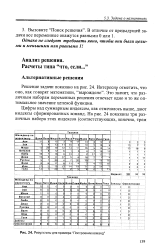 |
Результаты для примера Построение команд. [32] |
Это значит, что различным наборам переменных решения отвечает одно и то же оптимальное значение целевой функции. [33]
Оказывается, что в задачах стохастического программирования с непрерывной вероятностной мерой Fm на и оптимальное значение целевой функции, достигаемое с помощью апостериорных решающих распределений, может быть достигнуто и на апостериорных решающих правилах. [34]
Если набор ( Л, Ь, с) содержит случайный элемент, то оптимальное значение целевой функции соответствующей задачи линейного программирования является случайной величиной. [35]
В основу метода положена идея последовательного улучшения некоторого начального решения, путем движения к оптимальному значению целевой функции, которое заранее неизвестно. [36]
Итак, в случае t0 0 каждая из двойственных задач имеет оптимальное решение, и оптимальные значения целевых функций равны. [37]
Практическое значение этого результата в том, что мы можем легко оценить, как изменится оптимальное значение целевой функции при изменении количества располагаемых ресурсов. В частности, если bi увеличивается на одну единицу, то следует ожидать увеличения целевой функции примерно на Я, единиц. Следует обратить внимание на то, что при этом нет необходимости решать новую задачу НЛП. [38]
F ( N - 1) и, наконец, F ( N), представляющее собой оптимальное значение целевой функции. В данном случае понятия переменных состояния и управляемых переменных совпадают, так что индекс не требуется. [39]
Если существуют решения для обеих частей двойной пары задач линейного программирования, то обе они имеют конечные и равные оптимальные значения целевых функций. [40]
Здесь также, если какая-нибудь из них имеет конечное решение, то и вторая имеет решение и оптимальные значения целевых функций равны. Приведенные две пары двойственных задач эквивалентны. [41]
Нетрудно было бы привести еще целый ряд примеров, показывающих, насколько по-разному влияет изменение величины ресурсов на оптимальное значение целевой функции для задач линейного и целочисленного линейного программирования. [42]
На каждой итерации ( обозначим ее t) имеется нижняя граница ( оценка), скажем х, оптимального значения целевой функции. Для упрощения изложения предположим, что на первой итерации значение х либо строго меньше оптимального значения, либо равно значению целевой функции, соответствующему фиксированному допустимому решению. [43]
В [ 355 и 357 ] соответственно для априорных и апостериорных решающих правил рассматриваются достаточные условия, при которых оптимальное значение целевой функции на смешанных стратегиях - решающих распределениях - достигается также с помощью чистых стратегий - решающих правил. [44]
Оптимизация газоперерабатывающих заводов усложняется двумя факторами: многомерностью задачи поиска экстремума, сложностью расчета целевой функции ГПЗ, равной сумме оптимальных значений целевых функций для элементов завода. [45]
Страницы: 1 2 3 4