Константа - скорость - элементарный процесс
Cтраница 1
Константы скоростей элементарных процессов в условиях равновесного энергетического распределения участвующих в химической реакции частиц по степеням свободы определяют из измерений концентрации реагирующих веществ и продуктов реакции. [1]
Задача о расчете констант скорости различных элементарных процессов может быть разделена на две части - динамическую и статистическую. В течение этого времени систему двух сталкивающихся молекул можно считать изолированной от всех остальных молекул и описывать ее состояние уравнениями механики, в которых учитываются степени свободы только этих молекул. [2]
С экспериментальной точки зрения нахождение константы скорости элементарного процесса является одной из самых фундаментальных задач. Эта задача решается без труда в случае простых реакций и неизмеримо усложняется в случае быстрых многостадийных процессов. За последние годы достигнут существенный прогресс в этом направлении, и исследование кинетики даже сложного процесса сегодня перестало быть камнем преткновения для исследователя. [3]
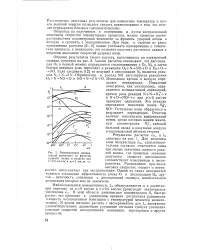 |
Распределение концентраций компонент за фронтом ударной волны в воздухе при. 7 5 кмIсек и р мм рт. ст. [4] |
Опираясь на полученные в измерениях и путем экстраполяции константы скоростей элементарных процессов, можно провести расчет распределения концентраций компонент за фронтом ударной волны в воздухе и сравнить с экспериментом. При этом, в отличие от ранее проведенных расчетов [2-4], важно учитывать одновременно и химические процессы, и ионизацию; это позволит получить расчетные данные в широком диапазоне скоростей ударных волн. [5]
В настоящее время имеется только весьма ограниченная информация о константах скоростей элементарных процессов частиц в определенных квантовых состояниях. В значительной степени по этой причине невозможно описать неравновесную кинетику, решая систему уравнений для. Как правило, с увеличением отношения Трел / Треак кинетика процесса все более усложняется. Исключительно эффективным методом измерения этих важнейших макроскопических параметров является метод ударных труб. Поэтому не удивительно, что половина представляемой вниманию советского читателя монографии Физическая химия быстрых реакций методически связана с ударными трубами. [6]
Необходимо учитывать, что различные механизмы реакции при соответствующем подборе значений констант скорости элементарных процессов могут давать сходные макрокинетические закономерности горения и, наоборот, для одного и того же механизма реакции зависимость ип от условий эксперимента может быть выражена различными уравнениями, в равной степени пригодными в пределах существующей точности эксперимента. Для решения же основных задач техники взрывобезопасности, которая пока остается главным прикладным объектом применения теории нормального горения, простая теория, не учитывающая особенностей цепного механизма, вполне достаточна. [7]
Эффект катализа или ингибирования может быть охарактеризован посредством множителя, состоящего из констант скорости единичных, элементарных процессов и концентрации катализатора или ингибитора. Результаты некоторых обобщений сравниваются с данными опыта. [8]
Исходя из общих положений химической кинетики, авторы работ [143, 151] установили, что константа скорости элементарного процесса рассматриваемого типа не может снижаться при повышении температуры. [9]
Третий цикл связан с традиционным стремлением Виктора Николаевича искать новые физические методы измерения констант скорости элементарных процессов, исследования механизмов сложных реакций. Мало известно, что именно Виктор Николаевич инициировал работы по применению ЭПР к исследованию атомных реакций в газах, которое дало столь много результатов в работах покойного В. В. Воеводского с сотрудниками, а затем А. Б. Налбандяна с учениками, причем в части этих работ Виктор Николаевич принял и непосредственное участие. [10]
Величина /, при которой интенсивность начинает влиять на выход продуктов, зависит от констант скорости элементарных процессов. [11]
Первые две экспоненты вместе с множителем к ( kT / h) представляют собой константу скорости элементарного процесса. [12]
В дальнейшем, используя различные зависимости наблюдаемых, эффективных жонстант, получают информацию о константах скорости элементарных процессов. [13]
Пусть далее k Aim ( и соответственно kf m и & f m) обозначает константу скорости элементарного процесса перехода из начального состояния ij в конечное состояние 1т при столкновениях молекул А и А. [14]
Такие системы ур-ний, в принципе, можно решать на ЭВМ, если имеются данные о константах скорости элементарных процессов мол. Для этого нужно определить наиб, быстрые параллельные и наиб, медленные последовательные переходы и вычислить ( или измерить) их константы скорости - величины, обратные временам жизни молекул в соответствующих возбужденных состояниях. [15]
Страницы: 1 2