Отрицательная асимметрия

Cтраница 1

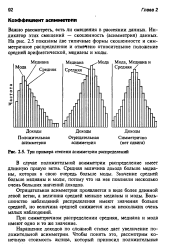Три примера степени асимметрии распределений. [1]

Отрицательная асимметрия проявляется в виде более длинной левой ветви, а величина средней меньше медианы и моды. Большинство наблюдений распределения имеют значения больше средней, но величина средней снижается из-за нескольких очень малых наблюдений. [2]

С возрастанием уровня напряжения влияние отрицательной асимметрии цикла становится существенней и СРТ значительно возрастает. Сопоставление последовательно снижаемого уровня напряжения на СРТ показало, что при достижении уровня напряжения 500 МПа отрицательная асимметрия цикла и пульсирующий цикл нагружения оказывают эквивалентное воздействие на рост трещины. Это связано с тем, что локальная асимметрия цикла нагружения, определяемая протеканием процесса пластической деформации перед вершиной концентратора напряжений, оказывается недостаточной для заметного влияния на процесс разрушения. Следовательно, определение закрытия вершины трещины в разных зонах вдоль фронта трещины при отрицательной асимметрии цикла должно быть осуществлено в зависимости от размера зоны пластической деформации. Для длинных трещин с возрастанием размера указанной зоны по длине трещины имеет место ослабление влияния отрицательной асимметрии цикла на СРТ. В области малоцикловой усталости ослабление роли отрицательной асимметрии цикла на рост малых трещин в пределах нескольких миллиметров от вершины концентратора напряжений происходит по мере снижения размеров формируемой перед ним зоны. [3]

Отметим, что третий момент распределения колебаний напряжения Рейнольдса обнаруживает сильную отрицательную асимметрию почти по всей толщине пограничного слоя. Значение эксцесса приближается к 10 в полностью турбулентной области и увеличивается до значений, больших 100 в области вязкого подслоя и на внешней границе пограничного слоя, в зоне перемежаемости. Распределение плотности вероятности на двух относительных толщинах пограничного слоя у / 8 ( приблизительно равным 30 и 8) приведено на рис. 16 для двух значений чисел Ree. Из этих двух рисунков видно отклонение закона распределения рейнольдсовых напряжений от нормального закона, характеризующееся подъемом для положительных значений и длинным шлейфом для, отрицательных значений ординат. [4]

Представленная закономерность отражает существенную роль зоны пластической деформации в эффектах влияния отрицательной асимметрии цикла на скорость роста трещины и ее закрытие. [5]

Изменяется только величина гладкой зоны, которая возрастает с переходом к отрицательной асимметрии цикла нагружения. Переход от отрицательной асимметрии цикла к пульсирующему циклу характеризуется изменением профиля усталостной бороздки. Она приобретает форму треугольника с меньшей стороной, обращенной к борозде предыдущего цикла нагружения с отрицательной асимметрией. Более того, указанная форма усталостной бороздки свидетельствует о том, что рост трещины в сторону магистрального направления начинается не в вершине, а на некотором расстоянии ( равном шагу усталостной бороздки) навстречу трещине. [6]

По данным табл. 1 оценка коэффициента асимметрии о-0 103, т.е. наблюдается отрицательная асимметрия. [7]

Если кривая плотности вероятности имеет пологий левый и крутой правый спад, распределение имеет отрицательную асимметрию. В этом случае для показателей центра распределения имеем: математическое ожидание медиана мода. [8]

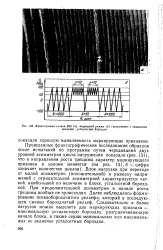Фрактогрймма сплава В95 ( а, маркерный режим ( б ( нагружение с заданными. [9]

Блок нагрузки при переходе от малой асимметрии ( положительной) к размаху напряжений с отрицательной асимметрией характеризуется четкой, наибольшей по величине в блоке, усталостной бороздкой. [10]

Первое подробное изучение дневных прибылей было предпринято Фамэ ( 1965а), который нашел, что прибыли имеют отрицательную асимметрию: большее количество наблюдений было на левом ( отрицательном) хвосте, чем на правом. [11]

Существующие модели формирования усталостных бороздок ( как было указано выше) не учитывают отмеченного явления и не позволяют объяснить увеличение шага усталостных бороздок при увеличении отрицательной асимметрии цикла нагружения. Более того, эти модели не позволяют объяснить появление дискретных сигналов АЭ на нисходящей ветви цикла нагружения. Перед вершиной трещины материал находится под действием сжимающих напряжений. [12]

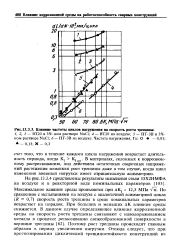Влияние частоты циклов нагружения на скорость роста трещины. [13]

В материалах, склонных к коррозионному растрескиванию, под действием остаточных сварочных напряжений растяжения возможен рост трещины даже в том случае, когда цикл изменения внешней нагрузки имеет отрицательную асимметрию. [14]

Из этой зависимости следует, что наиболее вероятное значение минимальной величины в выборках объемом т должно уменьшаться пропорционально ( log m) 1 / p и распределение минимальных величин должно иметь отрицательную асимметрию. Это означает, что статистическое описание физического явления, для которого справедлива гипотеза слабейшего звена, должно иметь асимметричное распределение прочности выборок одинакового объема и примерно полулогарифмическую зависимость наиболее вероятной величины прочности ( или эквивалентной ей характеристики) от размера образца или числа дефектов. Это и приводит к использованию асимметричных распределений и полулогарифмических зависимостей при изучении прочности материалов. [15]

Страницы: 1 2 3 4