Упругая конструкция

Cтраница 3

Эта расчетная схема применяется для упругих конструкций с двумя сосредоточенными массами, для рамных фундаментов при раздельном учете упругости рамы и грунтового основания. [31]

При статическом моделировании напряженно-деформированного состояния упругих конструкций целесообразно в качестве независимых масштабов принять геометрический масштаб 10, масштаб упругих свойств Е0 и плотности р0 материала, а также масштаб относительных деформаций е0, положив последний равным единице. [32]

Таким образом, потенциальная энергия упругой конструкции, подчиняющейся закону Гука, является однородной квадратичной формой координат точки, отсчитываемых от положения ее при недеформированном состоянии конструкции. [33]

Буровая платформа ферменного типа для установки в Мексиканском заливе.| Вариант схематизации стальной опоры плоской фермой. [34]

Принято, что в динамически нагруженной упругой конструкции стержни удлиняются и деформируются по статической форме изгиба от перемещений своих концов. [35]

Скачок при постоянном объеме, возникающий при коллапсе замкнутой сферической оболочки. [36]

Рассмотрим ровный ветер, обдувающий гибкую упругую конструкцию. Он может вызывать и поддерживать колебания с большой амплитудой, похожие на те, которые разрушили подвесной мост Такома Нэрроуз ( Tacoma Narrows), показанный непосредственно перед разрушением на фото 11 гл. [37]

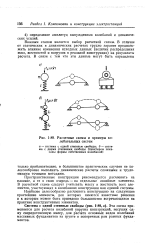Расчетные схемы и примеры колебательных систем. [38]

Эта схема применяется для расчета колебаний упругих конструкций, несущих одну сосредоточенную массу, для расчета основных видов колебаний массивных фундаментов на грунте и поперечных рам рамных фундаментов. [39]

Исторически и логически исследование потери устойчивости упругих конструкций представляет центральную главу теории устойчивости. Рассмотрение простых физических моделей упругих конструкций является прекрасным введением к дальнейшим более специальным вопросам. [40]

В настоящем параграфе излагается асимптотическая теория армирования упругих конструкций стержнями с точечными связями. Теория излагается параллельно с решением простейших типичных задач. [41]

Рассмотрим напряжение т кПмг, возникающее при деформации упругой конструкции под действием веса и заданного распределения нагрузок. [42]

Том третий посвящен расчету колебаний элементов и систем упругих конструкций. В нем даны методы расчета систем, состоящих из прямых и криволинейных стержней, пластин и оболочек, расчет важнейших конструктивных элементов - валов, пружин, турбинных и компрессорных лопаток, дисков, колец. Описаны способы оценки выносливости конструктивных элементов, подверженных вибрациям, методы определения вибраций в газовых и паровых турбинах, двигателях внутреннего сгорания, станках, автомобилях и в других машинах и агрегатах. Рассмотрены методы построения расчетных моделей. [43]

Этот принцип гласит, что если потенциальная энергия упругой конструкции ( линейной или нелинейной) представляется функцией от неизвестных перемещений узлов, то конструкция будет находиться в состоянии равновесия, когда перемещения имеют такие значения, при которых полная потенциальная энергия принимает стационарное значение. Обычно конструкция находится в состоянии устойчивого равновесия, и тогда полная потенциальная энергия минимальна. При этих условиях уравнения (11.63) представляют собой запись принципа минимума потенциальной энергии. Для неустойчивых конструкций потенциальная энергия может иметь либо максимальное, либо нейтральное значение. [44]

Это выражение для полной потенциальной энергии справедливо для любой упругой конструкции независимо от того, как она себя ведет - линейно или нелинейно. [45]

Страницы: 1 2 3 4