Маллинза

Cтраница 1

Маллинза уравнение 233 Маллинза - Патрикеева Эффект 234 Метод золь - гель анализа 221 ел. [1]

Свячь между энергией разрушения и характеристиками рассеянной механической энергией. [2]

Маллинза [369] - для характеристической энергии раздира; б - по данным Гроша и др. [535] - для энергии разрыва ( для резин на основе различных типов каучуков и наполнителей), при разных температурно-скоростных условиях. [3]

Схематическая иллюстрация теорий размягчения под напряжением. [4]

Маллинз и Тобин [653]; б - Бики [154]; в - Да ненберг [209] и Бунстра ( 108 ] ( цепи, испытавшие скольжение, отмечены метками); / - исходное равновесное состояние; 2 - полное выпрямление самой короткой цепи; 3-скольжение цепи; 4 - расположение макромолекул, обеспечивающее высо кий модуль, выравнивание напряжений; 5-исходное состояние после предварительного растяжения; 6 - упругое восстановление. [5]

Маллинз и Хирс [208] разработали детальную микроскопическую кинематическую теорию, выписав в явном виде систему дифференциальных уравнений, каждое из которых соответствует движению одной ступени. Получены некоторые новые выводы относительно поведения конечных эшелонов ступеней, хвостовая часть которых, как оказалось, разбивается на эшелон с двойными ступенями. [6]

Маллинз и Гомонофф сделали обзор ряда испытаний моделей запасов применительно к управлению денежными средствами. [7]

Маллинз считает, что эффект размягчения резин при больших деформациях не связан с разрушением пространственной структуры наполнителя по той простой причине, что разрушение таких структур происходит при малых деформациях. Это утверждение не противоречит данным, приведенным в предыдущем разделе. Процесс нелинейной вязкоупругости при малых деформациях связан с а - релак-сацией, когда адсорбционные слои полимера на активном наполнителе ( твердая составляющая) размягчаются, а отдельные части и частицы суперсетки активного наполнителя, связанные между собой адсорбционными силами, распадаются. Распадаются узлы 4 ( см. рис. 8.3), а узлы 3 не нарушаются. Одновременно исчезают и контакты между частицами ( агрегатами) наполнителя. [8]

Маллинз и Гомонофф сделали обзор ряда испытаний моделей запасов применительно к управлению денежными средствами. [9]

Маллинз, исходя из феноменологического описания процесса деформации, считает, что деформационные свойства наполненных вулканизатов могут быть описаны моделью, согласно которой резина состоит из двух фаз, причем основная деформация происходит в мягкой фазе, имеющей деформационные характеристики ненаполненного вулканизата. Деформация увеличивает долю вул-канизата, находящегося в мягкой фазе, в результате деструкции относительно нерастяжимой твердой фазы. Такая простая модель позволяет объяснить не только размягчение наполненных резин при растяжении, но и резкий подъем кривой напряжение - деформация при растяжениях, близких к максимальным. Резкий, подъем вызывается тем, что вулканизат в мягкой фазе подвергается высоким деформациям, близким к максимальным. Недостаток этой модели заключается в том, что предположение о жестких и мягких областях не связывается с реальными молекулярными параметрами полимера. [10]

Особенности проявления эффекта Маллинза тесно связаны с химической природой эластомера. [11]

Маллинза уравнение 233 Маллинза - Патрикеева Эффект 234 Метод золь - гель анализа 221 ел. [12]

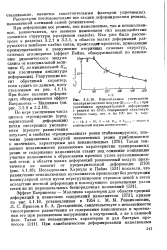Относительное уменьшение квазиравновесного модуля (. оэ - Ясс при увеличении предварительной деформации е резины из СКВ, содержащей канальную газовую сажу, вес. ч. на 100 вес. ч. каучука. [13]

Эффект Патрикеева - Маллинза характерен для области средних деформаций и невысоких содержаний наполнителя [373]; кривая на рис. 4.1.18, установленная в 1954 г. М. М. Резниковским, Л. С. Приссом и Б. А. Догадкиным, свидетельствует о независимости тиксотропного размягчения от содержания наполнителя и протекания его при равновесном нагружении в каучуковой, а не в сажевой фазе. [14]

Концепция Бикки объясняет эффект Маллинза - Патрикеева, так как цепи, разрушенные во время первого цикла, при втором цикле не будут влиять на деформацию резины ( до точки А, рис. 8.32), а цепи, не разрушенные при первой деформации ( до точки А), будут влиять на дальнейшую деформацию ( до точки Б) как и при первом цикле растяжения. Расхождение точки зрения Бикки со взглядами других исследователей касается деталей. Бикки считает, что в основном происходит разрыв самих цепей, тогда как многие другие [113-117] считают, что разрыв напряженных цепей происходит по местам их контакта с частицами активного наполнителя. Последняя точка зрения представляется автору наиболее вероятной. [15]

Страницы: 1 2 3