Интегральный масштаб

Cтраница 3

Расчет скорости диссипации, интегрального масштаба турбулентности и внутренних масштабов турбулентности в опытах показывает ( табл. 2), что по длине струи скорость диссипации падает, а интегральный масштаб турбулентности возрастает. Последнее обстоятельство является следствием затухания прежде всего мелкомасштабной турбулентности. Скорость наименьших вихрей v0 падает по длине струи, а масштаб их г увеличивается. [31]

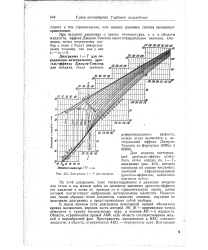Диаграмма i - 7 для воздуха. [32]

По этой диаграмме, зная теплосодержание и давление воздуха для точки п, мы можем найти по опытному значению дроссель-эффекта его давление в точке т, проводя от л горизонтальную линию, длина: которой соответствует выбранному интегральному масштабу. [33]

На рис. 2 даны зависимости нормированной величины lg ( iOOL / Df) от геометрических факторов. Нормированный интегральный масштаб L / Dr, характеризующий размеры энергосодержащих вихрей, зависит в основном от d: чем больше втулочное отношение, тем меньше L / DT. Изменение фактора / ко ( рис. 2, г) от 3 до 7 резко уменьшает отклик. Дальнейшее увеличение / ко не приводит к изменению отклика. [34]

Покажем теперь, что при 0 1 и L дс формула (5.29) дает правильный порядок величины с, т.е. условие (5.30) также несущественно. Так как интегральный масштаб турбулентности L много больше, чем Ьс, а колмо-горовский масштаб г. много меньше, чем 6С, то размер дс принадлежит инерционному интервалу. [35]

Интегральные масштабы и в газовой и жидкой фазах при различных глубинах жидкости. [36]

Примечательно, что масштабы, подсчитанные по автокорреляционным функциям в одно - и двухфазном потоках, оказались выше рассчитанных по взаимокорреляционным функциям. Рассматривая совместно поведение интегральных масштабов в газовой и жидкой фазах, можно обратить внимание на снижение их по мере приближения к поверхности раздела фаз. Пока трудно достоверно объяснить это наблюдение. В качестве первого приближения можно допустить, что вблизи волн интегральный масштаб турбулентности формируется под воздействием возмущений, генерируемых при обтекании волн на поверхности раздела. Размеры вихрей почти всегда меньше геометрических размеров канала, но достаточно энергоемки. Свидетельством тому являются и результаты спектрального состава пульсаций скорости в рассматриваемой области течения, они указывают на наличие второго пика в спектре на частотах, близких к частоте волн на поверхности раздела. [37]

Экспериментально определены временные масштабы турбулентных пульсаций скорости и коэффициенты турбулентной диффузии в воздушных потоках разных типов. Найдена связь между временными интегральными масштабами в эйлеровой и лагранжевои системах координат. Обсуждается справедливость и универсальность различных соотношений для вычисления коэффициента турбулентной диффузии по результатам определения масштабов в эйлеровой системе координат. [38]

Здесь величина LQ есть интегральный масштаб турбулентности ( характерный масштаб движения среды), величина LI ( размер турбулентного моля) - масштаб внутреннего движения или состояния системы, а величина / о - молекулярный почти нулевой микромасштаб. [39]

Результаты вычислений интегрального масштаба по сечению однофазного потока в гладкой трубе, на которой изучалась структура двухфазного потока, приведены на рис. 2.29. Они оценивают продольный и поперечный интегральные масштабы на основании непосредственных измерений корреляций между продольными пульсациями скорости в точках, сдвинутых вдоль ц поперек потока. С удалением от стенки трубы интегральные масштабы возрастают, а в основной толще потока остаются почти неизменными. Следует отметить, что по всему сечению трубы поперечный интегральный масштаб пульсаций и почти вдвое меньше продольного. На рис. 2.29 приведены также результаты расчета интегрального масштаба пульсаций и по автокорреляционным функциям на основе гипотезы Тейлора о замороженной турбулентности. Как видим, получаются несколько отличные результаты. Особенно ощутима разница вблизи стенки, где течение характеризуется высоким уровнем турбулентности. [40]

Известно, что капли дисперсной фазы размером меньше микромасштаба турбулентности стремятся следовать за турбулентными вихрями любого масштаба. Однако если размер капель превышает интегральный масштаб турбулентности, то движение капель определяется полем осредненных скоростей. [41]

Хинце [197], рассматривая проблемы переноса в турбулентных потоках, ввел понятие жидкого моля, под которым понимает достаточно протяженную часть жидкого континуума, состоящую из когерентного конгломерата жидких частиц. Размер жидкого моля сравним с интегральным масштабом турбулентного движения, причем обмен его с окружающей средой будет определяться влиянием мелкомасштабных турбулентных движений. В процессе перемещения в радиальном направлении, совпадающем с направлением градиента давления и при противоположном движении, турбулентные моли совершают микрохолодильные циклы. В рамках формализма Прандтля предполагается, что каждый жидкий или, как его еще называют, турбулентный моль в процессе турбулентного движения представляет собой некоторую индивидуальность, сохраняющую свою субстанцию в течение некоторого характеристического промежутка времени. Необходимо помнить, что имеющие место пульсации давления при перемещении моля на длине пути смешения / будут сопровождаться переносом импульса. Тогда, если импульс не сохраняется, нарушается требование, предъявляемое Прандтлем к транспортабельной субстанции, - турбулентному молю. Тем не менее понятие турбулентного моля удобно использовать при анализе задач переноса. [42]

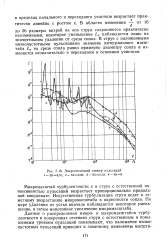Энергетический спектр пульсаций. [43]

Ьх наблюдается лишь на значительном удалении от среза сопла. В струе с наложенными низкочастотными пульсациями значение интегрального масштаба Lx на срезе сопла равно примерно диаметру сопла и изменяется незначительно в переходном и основном участках. [44]

Одни результаты получены по автокорреляционным функциям с использованием гипотезы замороженной турбулентности, другие - по взаимокорреляционным функциям. По-видимому, во втором случае результаты по интегральным масштабам более достоверны. [45]

Страницы: 1 2 3 4