Великий французский математик

Cтраница 1

Великий французский математик Анри Пуанкаре сравнивал собрание разрозненных фактов с грудой камней, из которых предстоит построить здание. Чтобы получить возможность предсказывать, из фактов нужно вывести упрощенную модель, или теорию, явления. Затем эту модель надо подвергнуть жестокой проверке, испытать ее на прочность, как гнут палку, пока та не сломается. Когда модель наконец не выдержит проверки, нужно попытаться построить новую теорию, учитывая и те факты, которые были раньше, и те, которые появились в ходе проверки. [1]

Это неравенство, которое обычно связывают с именем великого французского математика XJX века О. Коши, бывает очень полезно при доказательстве многих неравенств. [2]

Это неравенство, которое обычно связывают с именем великого французского математика XIX века О. Коши, бывает очень полезно при доказательстве многих неравенств. [3]

Это неравенство, которое обычно связывают с именем великого французского математика XIX века О. Коши, бывает очень полезно при доказательстве многих неравенств. [4]

Симон Дени Пуассон ( 1781 - 1840) - великий французский математик. [5]

Это неравенство называют также неравенством Коши - по имени великого французского математика XIX века, Доказательство неравенства Коши приводится в § 3 гл. [6]

Это неравенство называют также неравенством Коши - по имени великого французского математика XIX века. Доказательство неравенства Коши приводится в § 3 гл. [7]

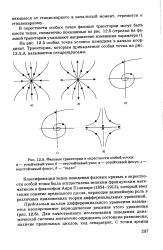Фазовые траектории в окрестности особой точки. а - устойчивый узел. б - неустойчивый узел. в - устойчивый фокус. г - неустойчивый фокус. д - седло. [8]

Классификация типов поведения фазовых кривых в окрестности особой точки была осуществлена великим французским математиком и философом Анри Пуанкаре ( 1854 - 1912), который ввел также понятие предельного цикла, играющее важнейшую роль в различных приложениях теории дифференциальных уравнений. [9]

Оператор V2 произносится как набла в квадрате и называется оператором Лапласа в честь великого французского математика. Уравнения, в которых утверждается, что лапласиан функции равен нулю, называются уравнениями Лапласа, а функции, которые подобно е и 0 удовлетворяют им, называются гармоническими функциями; ниже будет дано много примеров с этими функциями. [10]

В этом параграфе будет определено и до некоторой степени изучено понятие предельного цикла, введенное великим французским математиком Пуанкаре, а также дан один критерий, позволяющий в некоторых случаях установить существование предельного цикла. Понятие предельного цикла играет важнейшую роль как в самой теории обыкновенных дифференциальных уравнений, так и в ее приложениях к технике. [11]

Паоло Руффини ( 1799 г.) и норвежца Нильса Генрика Абеля ( 1824 г.) к исследованиям великого французского математика Эвариста Галуа ( 1830 г.), у которого идея группы используется уже достаточно сознательно - им же был введен и сам термин. [12]

Для построения множества Gf в виде (3.24) предлагается использовать методы теории линейных неравенств, разработка которой, была начата еще в начале XIX века в работах великого французского математика Жана Батиста Фурье. Поскольку эти методы недостаточно известны широкому кругу читателей, дадим общее представление о некоторых идеях этой теоршт. [13]

Гравитационное поле тем сильнее, чем больше масса тела и чем меньше размер области пространства, в которой это тело сосредоточено. Еще в 1795 г. великий французский математик Пьер-Симон Лаплас, исследуя распространение света в поле тяготения, пришел к выводу, что в природе могут встречаться тела, абсолютно черные для внешнего наблюдателя. Поле тяготения таких тел настолько велико, что не выпускает наружу лучей света. На языке космонавтики STO означает, что вторая космическая скорость была бы больше скорости света с. [14]

Существует простой способ решения подобной проблемы, включающий ограничения на область изменения переменных. Этот способ был открыт великим французским математиком Жозефом Луи Лагранжем ( 1736 - 1813) и носит название метода неопределенных множителей Лагранжа. [15]

Страницы: 1 2