Циклически стабильный материал

Cтраница 2

Циклический предел пропорциональности ST определяемый по допуску на остаточную деформацию 0 01 %, также изменяется в зависимости от типа материала и поцикловой трансформации петли гистерезиса - ST растет у циклически упрочняющихся материалов, уменьшается у разупрочняющихся и неизменен у циклически стабильных материалов. [16]

Следует, обратить внимание на эффективность применения в расчетах при неизотермическом нагружении [ 5 ] схематизированных диаграмм деформирования, полученных приближенным способом на основании изотермических диаграмм, соответствующих крайним температурам термического цикла с использованием принципа Мазинга. Однако этот подход применим для циклически стабильных материалов и не может быть распространен на циклически упрочняющиеся и разуп-рочняющиеся материалы. [17]

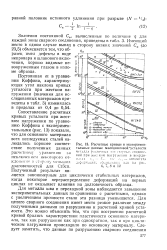Расчетные кривые и экспериментальные данные малоцикловой усталости. [18]

Полученный результат является закономерным для циклически стабильных материалов, когда некоторое перераспределение деформаций на первых циклах не оказывает влияния на долговечность образца. [19]

Основная проблема состоит в надлежащем выборе аргументов функции Q с тем, чтобы наилучшим образом отразить повреждения, накапливаемые на различных этапах сложного цикла. Ограничимся здесь случаем регулярного циклического нагружения циклически стабильного материала ( в таком состоянии материал обычно находится на большей части долговечности конструкции. [21]

Анализ диаграмм циклического деформирования показал, что исследуемые материалы обладают контрастными циклическими свойствами при комнатной температуре. Сталь 22К при симметричном цикле нагружения является циклически стабильным материалом. Ширина, петли, уменьшаясь в первые циклы ( N 5), остается неизменной по числу циклов нагружения ( рис. 3, а) и лишь при больших значениях исходных деформаций ( е) 22; все деформационные характеристики даны в относительных величинах к деформации на уровне предела пропорциональности в нулевом полуцикле) в области квазистатических разрушений материал начинает разупрочняться. На рис. 3, б показано изменение ширины петли с числом циклов нагружения для теплостойкой стали ТС. [22]

ОНС, реализующегося у вершины трещины, имеет ряд отличительных особенностей от случаев одноосного или плоского напряженного состояния. В частности, оказывается, что даде для циклически стабильного материала размахи пластической и упругой деформации в цикле зависят не только от размаха нагрузки, но и от ее максимального значения. [23]

Рассмотрим некоторые свойства модели с обратимым упрочнением. Исходя из выражений (5.1), (5.6), (5.8), можно показать, что, как и в случае модели циклически стабильного материала, анализ поведения которой был дан в предыдущих главах, здесь обнаруживается стремление скорости ползучести при длительной выдержке ( r const, Т const) к некоторому стационарному значению. [24]

С учетом этих данных оказалось возможным сформулировать обобщенный принцип подобия, охватывающий как склерономные, так и реономные свойства циклически стабильных материалов. Соответствующие уравнения состояния отражают систему довольно простых правил, позволяющих со степенью приближения, вполне достаточной для инженерных расчетов, определить ход диаграммы деформирования и кривой ползучести при произвольной истории пропорционального повторно-переменного на-гружения. [25]

Образцы для испытаний на.| Гладкие образцы для испытаний на малоцикловую усталость. [26]

С связан с пластичностью при разрушении, вызванном статическим растяжением. При циклическом нагружении с заданным размахом напряжения ( см. рис. 6, б) р процессе испытания сохраняются постоянными значения 0тах и own, ширина же петли гистерезиса от цикла к циклу может изменяться в зависимости от особенностей материала: уменьшаться для циклически упрочняющихся материалов, увеличиваться - для циклически раз-упрочняющихся материалов и, наконец, сохраняться неизменной для циклически стабильных материалов. При этом процесс накопления пластических сдвигов может, рообще говоря, происходить вплоть до разрушения. [27]

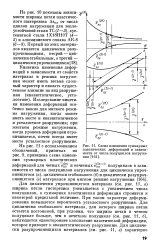Схема изменения суммарных. пластических деформаций в зависимости от числа полуциклов нагружения. [28]

Для циклически упрочняющегося материала ( см. рис. 11, а) ширина петли гистерезиса уменьшается с увеличением числа полуциклов, а суммарная пластическая деформация стремится к некоторой предельной величине. При таком характере деформирования повышается вероятность усталостного разрушения. Для циклически стабильного материала, для которого ширина петли остается постоянной, при условии, что ширина петли в четном полуцикле больше, чем в нечетном полуцикле ( см. рис. И, б) наблюдается одностороннее накопление пластической деформации, которое приводит к квазистатическому разрушению. [29]

Уравнение (9.83) принимается как основное для определения предельного числа циклов при циклическом изменении напряжений в условиях линейного напряженного состояния. При этом предполагается, что пластическая деформация не изменяется от цикла к циклу. Однако такое допущение справедливо только для циклически стабильных материалов. [30]

Страницы: 1 2 3