Идеально упругий материал

Cтраница 3

Эти примеры убеждают нас в том, что в области конечных деформаций можно создать одну и ту же деформацию, или деформированное состояние идеально упругого материала, посредством двух ( или более) типов нагружения, зависящих от пути, по которому деформировалась среда. Иными словами, данное состояние конечной деформации, вообще говоря, без указания определенного пути деформирования еще не определяет единственным образом напряженного состояния даже в идеально упругой среде в тех случаях, когда происходит поворот главных направлений напряжений или деформаций или тех и других относительно материала. Следовательно, мы должны ожидать, что механическая работа, требуемая для проведения разных последовательностей деформирования, завершающихся одним и тем же конечным состоянием деформации, не обязательно будет одной и той же. [31]

Поглощающая способность муфты определяется свойствами материала деформируемых деталей ее. Идеально упругий материал характеризуется зависимостью сил сопротивления только от в е-личины деформации, работа деформации материалом не поглощается. Этим свойством в дос гаточной степени обладает сталь, из которой изготовляются деформируемые детали упругих муфт. Работа, затрачиваемая на относительный поворот валов, поглощается муфтой в незначительной степени, что обеспечивает малые потери энергии и незначительный нагрев муфты, а в со-че: аниисо снижением жесткости кинематической цепи может привести к величению амплитуды кгугильных колебаний и медленному их га-ше. [32]

Он отмечает, что эти уравнения не зависят от закона, определяющего усилия и удлинения в волокнах. Приняв идеально упругий материал, следующий закону Гука вплоть до разрушения, и рассматривая элемент ofhn у заделанного конца, он полагает, что под изгибающим воздействием нагрузки р плоскость / / г примет положение gm и малые треугольники fge и emh изобразят деформации и напряжения волокон. [33]

Чтобы за - L мКнуть систему, требуются уравнения состояния ма - t териала. Термодинамическое состояние несжимаемого идеально упругого материала полнЪстью определяется заданием градиента перемещения к j, а следователь - но, и деформации, а также некоторой термической. [34]

При заделке трещин в бетонных покрытиях имеются попытки вместо стальных стержней использовать пряди и стержни из стек-ловолокна совместно с пластбетоном. Стекловолокно является почти идеально упругим материалом, его модуль упругости почти в 3 раза меньше, чем у высокогорочной стальной арматуры. Под этой прокладкой нет сцепления между плитой и полимерным материалом и, таким образом, вместо трещины образуется шарнирное соединение. Лучший результат дает применение стеклопласти-ковых стержней прямоугольного сечения. Этот способ целесообразен, если предварительно плита усилена нагнетанием песка в основание или другим методом. [35]

Зависимость деформации от времени при постоянном напряжении для материала, обнаруживающего мгновенную упругость, запаздывающую упругость в течении. [36]

В случаях, когда можно пренебречь тем или иным членом этого выражения, зависимость существенно упрощается. Полимер ведет себя подобно идеально упругому материалу с модулем Gx. [37]

Уравнения (3.11) и (3.12) образуют совместно основные уравнения линейной теории упругости и определяют поведение всех возможных упругих элементов. Конечно, эти соотношения относятся к идеально упругому материалу. Как показывает опыт, характеристики реальных материалов заметно отличаются от идеальных характеристик, а размер отклонения непосредственно определяет качество датчика силы. Поэтому свойства материалов упругих элементов имеют решающее значение для всех датчиков первого типа. [38]

Изгиб стержня прямоугольного сечения в упруго-пластической стадии. [39]

С учетом пластической деформации напряжения, превосходящие предел текучести при расчете для идеально упругого тела, снижаются. Если эпюра распределения напряжений для действительного материала и для идеально упругого материала отличаются одна от другой ( при одшьх и тех же нагрузках), то в теле после снятия внешней нагру. В местах наибольших напряжений остаточные наиряже-ния противоположны по знаку напряжениям в рабочих условиях. [40]

Распределение напряжений.. ри действии предельного пластического момента. [41]

С дне-том пластической деформации напряжения, превосходящие предел текучести при расчете для идеально упругого тела, снижаются. Если эпюры распределения напряжений для действительного материала и для идеально упругого материала отличаются одна от другой ( при одних и тех же нагрузках), то в теле после снятия внешней нагрузки возникают остаточные напряжения, эпюра которых представляет собой разность эпюр упомянутых напряжений. [42]

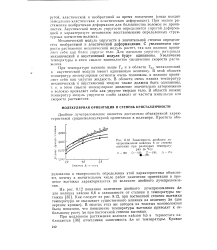Зависимость двойного лучепреломления найлона 6 от степени вытяжки при различных температурах ( в С. [43]

Механический модуль упругости в значительной степени определяется необратимой и эластической деформациями. С увеличением скорости растяжения механический модуль растет, так как волокно проявляет себя как более упругое тело. Для идеально упругого материала механический и акустический модули будут одинаковы. Увеличение температуры в этом смысле эквивалентно увеличению скорости растяжения. [44]

Среди недавно полученных соединений кремния ( силиконов) имеются такие разновидности, которые текут под действием собственного веса. Шар, который легко деформируется простым нажатием руки, растекается под действием собственного веса, если оставить его в покое на столе. Если тот же шар бросить с небольшой высоты, 1 - 2 м, на пол то он отскакивает, обнаруживая в высокой степени свойство упругости. Под очень быстро действующей нагрузкой силикон ведет себя подобно идеально упругому материалу; под небольшими же статическими нагрузками он деформируется медленно и необратимо и течет, как вязкая жидкость. [45]

Страницы: 1 2 3 4