Матрица - план
Cтраница 1
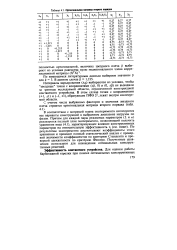
Матрица плана представляет собой прямоугольную таблицу, содержащую информацию о количестве и условиях проведения опытов. Строки матрицы плана соответствуют опытам, а столбцы - факторам. [1]
Пусть матрица плана X фиксирована. [2]
Пусть матрица плана Z обладает свойством, что ее строки ортогональны. [3]
Дополним матрицу плана столбцом значений отклика у, полученных в опытах. [4]
При записи матрицы плана обычно переходят к новой системе координат, что резко упрощает форму записи и обработку результатов наблюдений. Этот переход называется кодированием и заключается в следующем. Выбирают центр планирования - некоторую точку в факторном пространстве, принимаемую за начало новой системы координат. Задаются интервалами варьирования факторов А - для Xi, которые должны быть заметно больше, чем ошибки измерения и фиксирования соответствующих Xi, но не должны выходить за пределы изучаемой области. Выбранную величину А принимают за единицу масштаба по соответствующей оси. [5]
В линейных моделях матрица плана X рассматривается как известная и фиксированная. Однако в некоторых областях статистических исследований, таких, как измерения траекторий в физике элементарных частиц, регистрация составляющих сложных химических реакций и др., значения объясняющих переменных X нельзя фиксировать строго и их приходится рассматривать как неизвестные средние регистрируемых случайных величин, значения которых меняются в соответствии с некоторым распределением от одного элементарного измерения к другому. Обе последовательности ( лг, t / j) рассматриваются как случайные, они как бы сливаются с точки зрения методического подхода к их трактовке. Соответствующие модели, следуя Фришу, называют конфлюентными1, а методы их изучения - конф-люентным анализом. [6]
Пусть X - матрица плана D ранга k ] первого порядка ( для k переменных, N точек), удовлетворяющая условиям ( В. [7]
 |
Ортогональная матрица второго порядка. [8] |
В соответствии с матрицей плана эксперимента исследуются все варианты конструкций в выбранном диапазоне нагрузок по фазам. По результатам эксперимента рассчитывают коэффициенты этого уравнения и проводят полный статистический анализ с проверкой значимости коэффициентов по критерию Стьюдента и проверкой адекватности по критерию Фишера. Полученные уравнения используют для нахождения оптимальных конструктивных решений. [9]
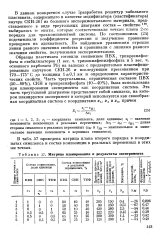 |
Матрица планирования и результаты эксперимента. [10] |
В табл. 57 приведена матрица плана второго порядка в координатах симплекса и состав композиции в реальных переменных в этих же точках. [11]
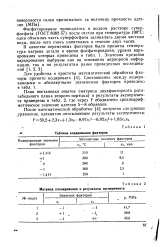 |
Матрица планирования и результаты эксперимента. [12] |
План постановки опытов ( матрица двухфакторного рота-табельного плана второго порядка) и результаты эксперимента приведены в табл. 2, где через У обозначено среднеарифметическое значение адгезии 5 - 8 образцов. [13]
Опыты будем выполнять согласно матрице плана, приведенной в табл. 6.3, в случайной последовательности, а в каждой точке плана повторим их 3 раза. Далее вычислим построчные дисперсии (6.6), проверим их однородность по критерию Кохрэна - ( см. гл. Коэффициенты уравнения (6.11) вычисляются по формуле (6.5), после чего по выражению (6.8) находятся их дисперсии и по критерию Стьюдента ( см. гл. [14]
Взвешивание типа 2 соответствует матрице плана D diu с элементами - 1, 0 и 1 - При этом и-я строка D отвечает и-му взвешиванию на весах, а г - й столбец отвечает г - му предмету. U - 1, если в и-и взвешивании г - й предмет положен на левую чашку весов; diu 0, если г - й предмет не участвует в и-ж взвешивании; diu 1, если г - й предмет в и-м взвешивании положен на правую чашку весов. [15]
Страницы: 1 2 3 4