Матрица - данные
Cтраница 1
Матрица данных из файла номер 10 нормируется программой НОРМА по координатам. [1]
Матрица данных и ее параметры, записанные в файл с номером 10, считываются программой ЛИРИСК с помощью подпрограммы DIN ( описание подпрограммы DIN приведено в § 1 гл. [2]
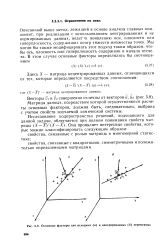 |
Основные факторы для исходных ( а и центрированных ( б переменных. [3] |
Матрица данных, посредством которой осуществляются расчеты основных факторов, должна быть, следовательно, выбрана с учетом свойств изучаемой химической системы. [4]
Пусть матрица данных ( таблица 4) имеет следующий вид. [5]
СОВА: матрица данных уже была пересчитана в базис собственных векторов. [6]
Факторный анализ матрицы данных ( х) позволяет определить р новых переменных, которые являются линейной комбинацией р исходных переменных и дают общую дисперсию. [7]
Здесь А - матрица данных N0 на NV, S - задаваемый ( вводимый) вектор, задающий подпоследовательность А. [8]
Анализируемые признаки в матрице данных могут быть измерены в разных шкалах - количественной, качественной ( ординальной) или номинальной ( см. гл. Некоторые значения могут быть вообще не определены. [9]
В предположении, что матрица данных X является неслучайной, возможны две точки зрения на оценку уравнения регрессии, полученную после отбора существенных предсказывающих переменных. [10]
Чему равны собственные значения матрицы данных. [11]
Преобразования, проведенные с матрицей данных, будут очень важной стадией в определении последующей обработки. Этот выбор определяется природой и свойствами данных и существованием явных физико-химических моделей. Поскольку для таблицы однородных данных нормировка переменных не является обязательной [16], она становится крайне желательной для переменных с резко различающимися свойствами и порядком значений. [12]
В зависимости от особенностей числового представления матрицы данных при выполнении преобразования, определяемого выражением (6.6.2), может понадобиться интерполяция. [13]
Выбор класса функциональной зависимости, аппроксимирующей матрицу данных, осуществляется из соображений сохранения физического соответствия математической модели реальному объекту. Таким образом, механические параметры объекта могут быть определены по совокупности измеренных электрофизических параметров и наоборот, электрофизические параметры могут быть определены по известным значениям механических парамегров. [14]
Выбор класса функциональной зависимости, аппроксимирующей матрицу данных, осуществляется из соображений сохранения физического соответствия математической модели реальному объекту. Таким образом, механические параметры объекта могут быть определены по совокупности измеренных электрофизических параметров и, наоборот, электрофизические параметры могут быть определены по известным значениям механических параметров. [15]
Страницы: 1 2 3 4