Матрица - данные
Cтраница 2
Выбор класса функциональной зависимости, аппроксимирующей матрицу данных, осуществляется из соображений сохранения физического соответствия математической модели реальному объекту. Таким образом, механические параметры объекта могут быть определены по совокупности измеренных электрофизических пара метров. ЕГ качестве электрофизических параметров в математических моделях обычно выступают коэрцитивная сила Не, удельное электрическое сопротивление), относительная магнитная проницаемость (, остаточная индукция Вг, намагниченность насыщения Is и другие параметры. Но для измерения совокупности этих параметров необходимо применение разнообразных приборов, установок и датчиков, что делает практически невозможным использование многопараметровой модели для экспресс-оценки технического состояния оборудования в производственных условиях. [16]
Нижеследующий подход применим как для оценки пропусков в матрице данных, так и для оценки значений главных компонент у некоторого объекта Xi с пропущенными значениями. [17]
Диаграмма представляет собой определенную фигуру, которая строится на основе матрицы данных размером [ M N ], где N - количество серий значений ( далее серий), М - количество точек, замерами в которых получены значения серий. [18]
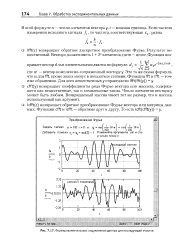 |
Формирование массива зашумленных данных для последующей очистки. [19] |
О icfft ( c) возвращает обратное преобразование Фурье вектора или матрицы данных, Функции cfft и icfft - обратные друг к другу. [20]
АФА позволяет определить число факторов, влиянием которых обусловлены наблюдаемые в матрице данных X изменения ее элементов, и восстановить с точностью до Ж эту матрицу данных с помощью элементов факторного разложения - матриц А и F - в координатном пространстве меньшей размерности. [21]
Вспомогательные модули выполняют обслуживающие функции: чтение управляющей записи, элементов и матрицы данных с устройства ввода с перфоленты и печать массива любого размера на алфавитно-цифровом печатающем устройстве. [22]
В случаях задачи отбора переменных это обстоятельство можно не учитывать, поскольку матрица данных не меняется и Ry. [23]
Потенциальный пользователь кластерного анализа должен также обратить внимание на то, что матрицы данных часто формируются различными способами. В биологии имеет место обратный порядок, что приводит к матрице данных размерностью PXN. [24]
Для упрощения анализа 2М - спектров иногда приходится изменять их представление либо путем преобразования матрицы данных в памяти компьютера, либо заменой метода получения данных. Некоторые из описанных в этом разделе способов изменения представления спектров используют теорему подобия фурье-преобразо-ваний, основанную на соотношении (6.4.17), которая связывает преобразование частотных переменных и соответствующее преобразование временных переменных. Другие методы используют свойства симметрии 2М - спектров. Более перспективные методы основываются на распознавании характерных структур пиков, что в конечном итоге позволит достигнуть полностью автоматизированной интерпретации 2М - спектров. [25]
Как указано в § 1.1, исходные данные могут быть заданы не только в виде матрицы данных, но и в виде матрицы близости ( расстояний) между объектами. Задача визуализации данных в этом случае тесно связана с методами так называемого многомерного метрического шкалирования [37], при котором стремятся построить некоторую матрицу данных ( конфигурацию точек) возможно меньшей размерности, объясняющую имеющуюся матрицу расстояний. [26]
Таким образом, решение нормальной системы уравнений для расширенной матрицы данных сводится к решению системы нормальных уравнений с центрированной матрицей данных не только теоретически, но и во многих случаях при практической реализации вычислительной процедуры. Отметим в связи с этим следующее. [27]
Естественно, что отсутствие четкого критерия достаточности и формальных методов получения порога значительно ограничивает возможности данного метода, особенно когда матрица данных плохо обусловлена и собственные значения у4 образуют плавную последовательность. Мерой обусловленности матрицы в данном случае может служить величина отношения максимального сингулярного значения к минимальному. [28]
Очевидна связь необходимой требуемой точности разложения по уравнению ( 5) с числом используемых в ФА собственных значений - чем точнее требуется восстановить матрицу данных, тем большее число собственных значений нужно для этого использовать. Однако, как уже было отмечено, строгих или хотя бы формальных критериев достаточности в данном методе нет. [29]
АФА позволяет определить число факторов, влиянием которых обусловлены наблюдаемые в матрице данных X изменения ее элементов, и восстановить с точностью до Ж эту матрицу данных с помощью элементов факторного разложения - матриц А и F - в координатном пространстве меньшей размерности. [30]
Страницы: 1 2 3 4