Экспериментальная матрица
Cтраница 1
Экспериментальная матрица Е количественно характеризует вероятностную зависимость а от величины а. Для наглядности ограничим анализ конечным рядом дискретных значений а и а, хотя на практике обе эти величины могут изменяться в некотором диапазоне значений непрерывно, и условные вероятности в экспериментальной матрице заменяются функциями условного распределения вероятностей. Чтобы получить возможность рассмотрения конкретного численного примера, допустим, что параметр а принимает лишь дискретные значения 1, 2 и 4 и меняется при изменении начальных условий в этих пределах. При подобном весьма упрощенном подходе экспериментальная матрица представляет собой набор условных вероятностей Р ( а / а) того, что при заданном значении а величина а приобретает некоторое конкретное значение. [1]
Экспериментальная матрица Е дает математическое описание шума. В дискретном случае, когда ( как в рассмотренном примере) существует лишь конечное число возможных уровней полезного сигнала и шума, матрица Е состоит из элементов, определяющих вероятность того, что при заданном полезном сигнале на входе системы получается суммарный сигнал данной величины. [2]
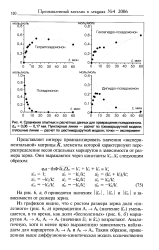 |
Сравнение опытных и расчетных данных для превращения псевдоионона. [3] |
Представляет интерес проанализировать значения экспериментальной матрицы А, элементы которой характеризуют перераспределение весов отдельных маршрутов в зависимости от размера зерна. [4]
Вообще говоря, в подобных случаях экспериментальная матрица дает количественное описание вероятностных соотношений в тех случаях, когда поступающая информация искажена или неполна: априорные вероятности попросту определяют вероятности различных событий ( или сигналов), которые фигурируют в задаче в качестве решений, а матрица потерь количественно определяет относительную цену ошибок. Поэтому теория решений применима при расчете нелинейных регуляторов, реализующих заданную нелинейную решающую функцию, причем решение принимается либо на основе измеряемой ошибки системы, либо на основе входного сигнала системы. [5]
Характеристики решающего устройства определяются: 1) экспериментальной матрицей Е, 2) априорными вероятностями, описываемыми матрицей-строкой Р, и 3) матрицей потерь L. Эти три матрицы количественно характеризуют лежащие в основе принятия решения факторы, о которых в общих чертах говорилось в разд. [6]
Правая часть этого неравенства, отношение правдоподобия, зависит от экспериментальной матрицы и априорных вероятностей. [7]
Таким образом, основными понятиями, используемыми в теории решений, являются экспериментальная матрица Е, матрица априорных вероятностей Р и матрица потерь L. Xh определяются dj), рассмотримту роль, которую играет каждая из трех рассмотренных выше матриц. Так как матрица Е описывает свойства шума или характер неопределенности, появляющейся при передаче сигнала или при измерениях, ее элементы часто можно оценить субъективно по известным статистическим свойствам этого шума. [8]
Поскольку учет влияния погрешностей эксперимента можно осуществлять с различной степенью строгости, определения ранга экспериментальных матриц разными способами не всегда приводят к совершенно одинаковым результатам. [9]
Входящие в правую часть этих уравнений величины L представляют собой как раз элементы матрицы потерь (15.27); условные вероятности являются элементами экспериментальной матрицы (15.24), а вероятности суть априорные вероятности соответствующих сигналов. [10]
Число таких признаков может быть относительно невелико. Поэтому в соответствующей экспериментальной матрице некоторые строки могут обладать одинаковыми значениями. [11]
Величина Рз2 равна вероятности того, что шум примет значение ( xz - 5з), если числа х и s соответственно определяют мгновенные значения суммарного входного и полезного сигналов. В любом случае элемент Paz и остальные элементы экспериментальной матрицы определяются только плотностью распределения вероятностей шумов, причем совокупность величин Рц фактически представляет собой количественное описание этой функции распределения. [12]
Экспериментальная матрица Е количественно характеризует вероятностную зависимость а от величины а. Для наглядности ограничим анализ конечным рядом дискретных значений а и а, хотя на практике обе эти величины могут изменяться в некотором диапазоне значений непрерывно, и условные вероятности в экспериментальной матрице заменяются функциями условного распределения вероятностей. Чтобы получить возможность рассмотрения конкретного численного примера, допустим, что параметр а принимает лишь дискретные значения 1, 2 и 4 и меняется при изменении начальных условий в этих пределах. При подобном весьма упрощенном подходе экспериментальная матрица представляет собой набор условных вероятностей Р ( а / а) того, что при заданном значении а величина а приобретает некоторое конкретное значение. [13]
Экспериментальная матрица Е количественно характеризует вероятностную зависимость а от величины а. Для наглядности ограничим анализ конечным рядом дискретных значений а и а, хотя на практике обе эти величины могут изменяться в некотором диапазоне значений непрерывно, и условные вероятности в экспериментальной матрице заменяются функциями условного распределения вероятностей. Чтобы получить возможность рассмотрения конкретного численного примера, допустим, что параметр а принимает лишь дискретные значения 1, 2 и 4 и меняется при изменении начальных условий в этих пределах. При подобном весьма упрощенном подходе экспериментальная матрица представляет собой набор условных вероятностей Р ( а / а) того, что при заданном значении а величина а приобретает некоторое конкретное значение. [14]
 |
Энергии ионизации примесей в кремнии ( в эВ, полученные из оптических данных. [15] |
Страницы: 1 2