Топологическая матрица

Cтраница 3

Пример информационного графа SDF-модели. [31]

Элемент ( j i) топологической матрицы ( j - номер строки, г - номер столбца) равен целому положительному числу О, если г-ж актор производит Oj токенов, передаваемых по j - й дуге. Элемент ( j, г) равен целому отрицательному числу - / г. если г-й актор потребляет / токенов по входящей j - й дуге. [32]

Таким образом, изучение свойств топологической матрицы А позволяет исследовать особенности сопряженных систем в рамках модели Хюккеля. Отсюда вытекает связь метода МОХ с математической теорией графов, обращение к которой позволило получить множество обобщений для класса сопряженных молекул. [33]

Алгоритм анализа динамических характеристик базируется на топологической матрице контур - ветвь ( F-матрице), описание и метод составления которой уже были приведены. F-матрица в общем виде представлена ниже. Столбцы матрицы разделены на четыре группы, соответствующие fC / L-ветвям. Строки матрицы также разделены на группы, соответствующие CRL У - связям. В обрамлении матрицы расположены параметры схемы. [34]

В методе МОХ матрица гамильтониана идентична топологической матрице молекулы, которая имеет единичные элементы в положениях, отвечающих связям С-С, и нулевые элементы во всех остальных положениях. [35]

Учет неконсервативных сжимающих сил в МГЭ обеспечивается топологической матрицей С, где каждый вариант поведения сжимающей силы имеет свой набор ненулевых компенсирующих элементов. [36]

В соответствии с видом уравнений Кирхгофа различают три топологические матрицы: матрицу соединений ( узловую) А, матрицу сечений Q и матрицу контуров В. [37]

Номер элемента системы NE есть номер его строки в топологической матрице ХТС. [38]

Поэтому матрицы, соответствующие этим определителям, называют также топологическими матрицами. Рассмотрим простую вековую задачу четвертого порядка. [39]

Метод узловых напряжений не требует построения дерева графа схемы и топологических матриц. Это обстоятельство делает формирование уравнений метода узловых напряжений более простым в сравнении с формированием уравнений методом сечений. [40]

В том и другом случае для представления уравнений Кирхгофа необходимы две разные топологические матрицы. [41]

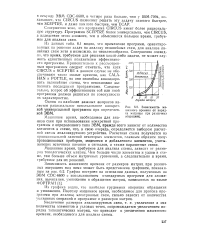Зависимость машинного времени от порядка матрицы при различных операциях. [42]

Машинное время, требуемое для анализа схемы, зависит от размеров топологических матриц. Чем больше число элементов и узлов в схеме, тем больше объем матричных уравнений, а следовательно и время, требуемое для их решений. [43]

Образование вырожденных координат в зависимости от. [44]

КК - При этом, как следует из приведенных соотношений, используются только топологические матрицы П [ П уП г ] и Р [ Р г / Р 2 ] относительно невырожденных координат. В то же время наличие вырожденных координат не снижает числа переменных в других типах уравнений. [45]

Страницы: 1 2 3 4