Исходная матрица

Cтраница 3

Преобразованная матрица Р системы уравнений. [31]

Из исходной матрицы S вычеркнуть ту строку, котор: я содержит этот ненулевой элемент и присоединить ее к матрице Р снизу. [32]

Преобразованная матрица Р системы уравнений. [33]

Из исходной матрицы S вычеркиваются те столбцы ( или столбец), которые для только что зачеркнутой строки содержат ненулевые элементы. Столбцы присоединяются к матрице Р слева. Если существуют несколько строк, для которых минимум р ( fj) одинаков и р ( fi) 1, то среди этих строк выбирается та, которая содержит переменные, входящие в наибольшее число уравнений. [34]

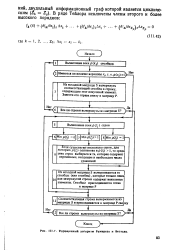Упрощенный алгоритм Рамиреза и Вестала. [35]

Из исходной матрицы S вычеркиваются те I столбцы ( или столбец), которые только лишь для зачеркнутой строки содержат ненулевые I элементы. [36]

Из исходной матрицы смежности [ S ] вычеркивают столбцы, отвечающие регламентированным переменным W, tj, fj и tj, и столбец, соответствующий переменной К ( конструкционный тип теплообменника), которая является оптимизирующей, поскольку, согласно проектному заданию, она может принимать лишь определенные дискретные значения. [37]

Умножив исходную матрицу на транспонированную слева, получаем информационную матрицу. [38]

Преобразовать исходную матрицу по правилу: четные строки разделить на полученное значение, нечетные оставить без изменения. [39]

К исходным матрицам следует добавить матрицы усилий отдельных элементов. Они необходимы при расчете пластин и оболочек, напряженное состояние которых характеризуется не сосредоточенными усилиями в расчетных сечениях, как при расчете стержневых систем, а распределенными. [40]

В исходной матрице А рамками обведены элементы, начиная с которых выполняется процедура слияния. Поэтому количество заполненных указателей в массиве L Q может оказаться меньшим, чем общее количество элементов в исходном массиве. [41]

К исходной матрице X добавляются две строки. Эти оценки представляют собой числа, которые учитываются тем или иным способом. [42]

По условию исходная матрица А есть результат возмущения ортогональной матрицы. Будем полагать, что матрица А в определенном смысле ( по норме) близка к ортогональной. Вследствие непрерывной зависимости собственных значений матрицы от вариаций элементов собственные значения Яд, матрицы С А А ( k 1, 2, 3) будут достаточно близки к единичным. [43]

Сначала составим исходные матрицы. Матрицу потенциала нагрузки (6.48) составим только для стержня BD, так как для остальных стержней эти матрицы нулевые. [44]

А - исходная матрица А с переставленными строками, а Е представляет собой матрицу ошибок округления. [45]

Страницы: 1 2 3 4