Результирующая матрица

Cтраница 1

Результирующая матрица содержит столько строк, сколько ограничителей в аргументе. [1]

Результирующая матрица представлена теперь произведением матриц, которому соответствует цепная схема рис. 8 - 16 6; в ней каждая параллельная ветвь состоит из единичного активного сопротивления. Если задана только функция 7 12, то первую и последнюю матрицы можно не принимать во внимание, так как они соответствуют ветви, параллельной входным зажимам, и ветви, последовательной с выходными зажимами. [2]

Результирующая матрица имеет па столбцов старшего разряда и п столбцов младшего, первые заполнены подкомбинациями из А, вторые - подкомбинациями из В. [3]

Результирующая матрица необходима для того, чтобы определить рисунок шкалы ККУ, но тот же рисунок будет получен при считывании символов элементарных матриц. [4]

Результирующая матрица имеет 18 столбцов и 400 строк, для ее построения следует выписать 7200 символов, но, как выше, было показано, рисунок шкалы может быть получен непосредственно при считывании элементарных матриц. [5]

Результирующая матрица хорошо согласуется с полученной при полном расчете самосогласованного поля. [6]

Результирующая матрица yl получена с помощью rkfixed и выведена в форме матрицы. В первом ее столбце, в соответствии с порядком перечисления аргументов в функции правых частей D, расположены значения времени t с шагом 0.5. Остальные столбцы матрицы yl содержат значения элементов вектора состояний. Выходная переменная zl ( см. рис. 3.24) также получена с привлечением вспомогательной матрицы HI. [7]

Программная реализация векторно-матричного рекуррентного выражения. [8]

Результирующая матрица в примере ( см. рис. 4.4) выведена в транспонированной форме, поэтому имеет два столбца и пять строк. [9]

Разложение для примера (. [10]

Результирующая матрица в примере ( см. рис. 5.47) имеет два вещественных собственных значения - положительное и отрицательное. Квадраты этих собственных значений также совпадают с собственными значениями исходной матрицы. [11]

Результирующая матрица подобна исходной матрице в пределах ошибок округления. [12]

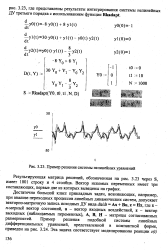Пример решения системы нелинейных уравнений. [13]

Результирующая матрица решений, обозначенная на рис. 3.23 через S, имеет 1001 строку и 4 столбца. Вектор искомых переменных имеет три составляющих, первые две из которых выведены на график. [14]

Результирующая матрица системы уравнений является ленточной симметричной и положительно определенной. Обычно в памяти ЭЦВМ хранится половина матрицы системы и используется подпрограмма решения системы линейных алгебраических уравнений прямым методом Гаусса или Холецкого для ленточной матрицы. Были проведены расчеты на модельной задаче при использовании прямых методов Гаусса и Холецкого и параллельно проведены расчеты для случая регулярного разбиения области Д /, когда для матрицы системы необходимо хранить в памяти только четыре ненулевых диагонали с использованием итерационного метода Гаусса - Зейделя. При равном числе элементов быстродействие программы метода Гаусса - Зейделя ( кривая I - 4t 2 5 с, tc Ю мин; кривая 2 - л1 5 с. [15]

Страницы: 1 2 3 4